Determine the approximate values of sinθ and cosθ from the diagram below

  • Context: MHB 
  • Thread starter Thread starter SarahJeen
  • Start date Start date
  • Tags Tags
    Approximate Diagram
Click For Summary
SUMMARY

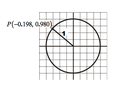
The discussion focuses on determining the approximate values of sinθ and cosθ based on a diagram, specifically referencing points on the unit circle centered at the origin. It establishes that x = cos(θ) and y = sin(θ), emphasizing that the exact values depend on the angle θ, which is not specified in the diagram. The conversation suggests a playful interpretation of θ as the angle related to the symmetry of the letter "o" in the Google logo, typeset in the Catull font.

PREREQUISITES
  • Understanding of trigonometric functions, specifically sine and cosine.
  • Familiarity with the unit circle concept in mathematics.
  • Basic knowledge of angles and their representation in diagrams.
  • Awareness of font types and their visual characteristics, such as symmetry.
NEXT STEPS
  • Study the properties of the unit circle and its relation to trigonometric functions.
  • Learn how to calculate sine and cosine values for various angles.
  • Explore the concept of angle measurement in different contexts, including radians and degrees.
  • Investigate the visual representation of angles in typography and design.
USEFUL FOR

Students of mathematics, educators teaching trigonometry, graphic designers interested in typography, and anyone looking to understand the relationship between angles and trigonometric functions.

SarahJeen
Messages
11
Reaction score
0
View attachment 863
The answer I got was: View attachment 864
If I'am wrong please explain the correct solution and explain your reasoning thanks sarah (Sun)
 

Attachments

  • Screen Shot 2013-06-01 at 9.12.40 PM.png
    Screen Shot 2013-06-01 at 9.12.40 PM.png
    6 KB · Views: 87
  • Screen Shot 2013-06-01 at 9.13.11 PM.png
    Screen Shot 2013-06-01 at 9.13.11 PM.png
    1.5 KB · Views: 86
Mathematics news on Phys.org
Re: Determine the approximate values of sinθ and cosθ from the digram below

If your points are on the unit circle centred at the origin, then [math]\displaystyle \begin{align*} x = \cos{(\theta)} \end{align*}[/math] and [math]\displaystyle \begin{align*} y = \sin{(\theta)} \end{align*}[/math].
 
SarahJeen said:
Determine the approximate values of sinθ and cosθ from the diagram below
This, of course, depends on what $\theta$ is since it is not marked on the diagram. Maybe it's the angle made by the axis of symmetry of the letter "o" in the Google logo (which is typeset in the Catull font). (Smile)

OCiJKUb.png
 

Similar threads

MHB Approximating Trig Values using the Unit Circle
  • · Replies 11 ·
Replies
11
Views
3K
Graduate Approximation with small parameter
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Why Is PQ Approximated as rΔθ in Small Angles?
  • · Replies 3 ·
Replies
3
Views
2K
MHB Stuck with probability question involving tree diagram?
  • · Replies 3 ·
Replies
3
Views
2K
MHB Determining all values of Θ (gr. 11 math)
  • · Replies 1 ·
Replies
1
Views
2K
MHB Finding the intersection points on the graph y=sinx, y=cosx and y=tanx
  • · Replies 4 ·
Replies
4
Views
9K
MHB What Determines the Time Dependent Value of A[t] in Quasi-Static Approximations?
  • · Replies 1 ·
Replies
1
Views
2K
High School Mass estimate only through mass rate of change
  • · Replies 4 ·
Replies
4
Views
2K
High School Fractional/decimal powers
  • · Replies 10 ·
Replies
10
Views
2K
Bisection and Newton's Approximation
  • · Replies 1 ·
Replies
1
Views
3K