Determine the Electrical potential at a given point

[Karl Karlsson]

Homework Statement

A rod with a circular center in the middle (which causes the rod to change direction by 90 °) has an evenly distributed linear charge density 𝜆 of electrons along the entire rod. Determine the electrical potential of the red dot in the figure below which is at the center of the circular round. The reference potential is 0 V far away from the rod.

Relevant Equations

See below

A rod with a circular center in the middle (which causes the rod to change direction by 90 °) has an evenly distributed linear charge density 𝜆 of electrons along the entire rod. Determine the electrical potential of the red dot in the figure below which is at the center of the circular round. The reference potential is 0 V far away from the rod.

Given values are radius R, length a and charge density 𝜆.

My attempt:

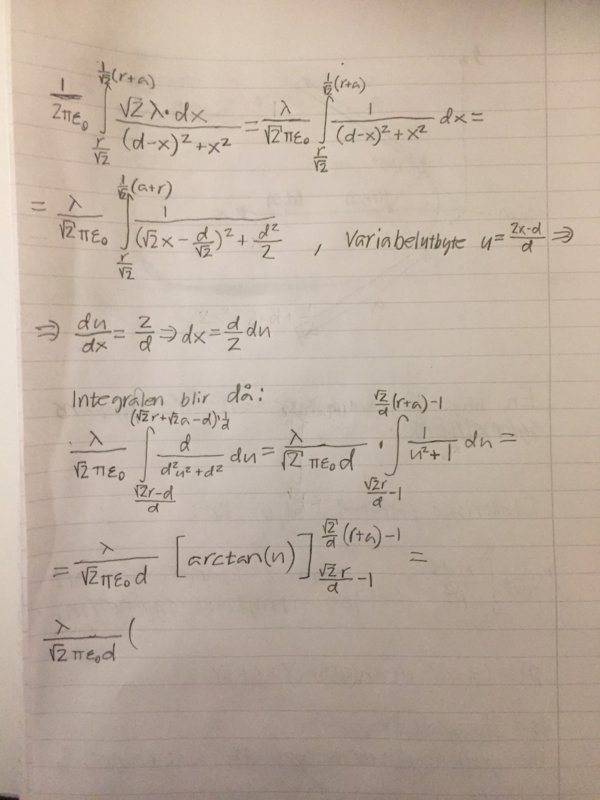
Sorry for writing my solution not in english but you get the idea. As one can see the integral gets very complicated when i am trying to come up with an expression for the force at point (d,0). And then i haven't even started doing the integral for the potential difference of the given point and point (d,0). There must be an easier way to solve this problem.

Thanks in beforehand!

 

[gneill]

The problem statement is asking for the potential at the dot, not the force.

Electric potential only depends upon the distance from a given charge and is a scalar value. The zero reference is assumed to be at infinity.

 

[kuruman]

I am not at all sure why you are concerned with the point you have labeled (d, 0). It is irrelevant. Note that the point of interest is at distance $R$ from the end of each straight segment in the perpendicular direction. Calculate the electric field vector potential contribution from one segment by integrating as suggested in the figure below, then superimpose the contribution from the other segment which has the same magnitude but different direction double it to account for the other segment, then calculate and superimpose the contribution from the quarter circle to its center.

Note: This post has been edited following @gneill's remarks in post #4.

 

[gneill]

Calculate the electric field vector contribution from one segment by integrating as suggested in the figure below, then superimpose the contribution from the other segment which has the same magnitude but different direction, then calculate and superimpose the contribution from the quarter circle to its center.

Still, the problem statement wants the electric potential at the point, not the field. Perhaps the OP (@Karl Karlsson) could confirm that the problem statement is correct?

Potential is easier to calculate since it's a scalar value, so no dealing with field component directions.

 

[kuruman]

Still, the problem statement wants the electric potential at the point, not the field. Perhaps the OP (@Karl Karlsson) could confirm that the problem statement is correct?

Potential is easier to calculate since it's a scalar value, so no dealing with field component directions.

Oops, yes, it is the potential. Good catch. I looked at OP's equations with the squares in the denominator and got side-tracked to think it is the field that needs to be calculated. Yes, the potential is easier. One has to double the potential from a single segment and the quarter circle potential is trivial because all the source points on it are equidistant from the point of interest. I edited post #3.

 

[Karl Karlsson]

Still, the problem statement wants the electric potential at the point, not the field. Perhaps the OP (@Karl Karlsson) could confirm that the problem statement is correct?

Potential is easier to calculate since it's a scalar value, so no dealing with field component directions.

Oops, yes, it is the potential. Good catch. I looked at OP's equations with the squares in the denominator and got side-tracked to think it is the field that needs to be calculated. Yes, the potential is easier. One has to double the potential from a single segment and the quarter circle potential is trivial because all the source points on it are equidistant from the point of interest. I edited post #3.

Of course now i see it, you are correct, it is much easier to calculate the potential by just plugging into the formula 1/(4pi*e0)*Q/r directly. I still get a quite difficult integral, could you review my solution, and thanks for the help!

Sorry for writing the text on a non english language but i think you understand by looking att the picture i drew and the mathematical expressions and thanks again!

 

[kuruman]

Your final answer agrees with mine. Good job!

 

[Karl Karlsson]

Your final answer agrees with mine. Good job!

Alright must be correct then. Thanks!