Determine the initial vertical reaction

[jjiimmyy101]

I solved the first one...

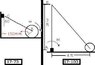
Problem 17-103 -- The two pin-connected bars each have a weight of 10 lb/ft. If a moment of M = 60 lb*ft is applied to bar AB, determine the initial vertical reaction at C and the horizontal and vertical components of reaction at B. Neglect the size of the roller at C. The bars are initially at rest. [By= 18.75 lb ; Cy = 31.25]

What I've done so far:

\sum Fx = max = 25(0.6) + Bx + 15(0.6) = 0
\sum Fy = may = -25(0.8) + Cy +By - 15(0.8) = 0
\sum MB = 0 = -60 -25(0.8)(2.5) + Cy(5) -15(0.6)(1.5)= 0

*I've taken my axis to be rotated (x-axis along BC, y-axis perpendicular to that)
* ax, ay, MB = 0 because it is initially at rest
*I've done something wrong (but I don't know what) because I keep getting the wrong answer. Any suggestions for this one?

Thanks for taking the time to read and answer this.

 

[member 553083]

The correct equations to use are: \sum Fx = 0 = 25(0.6) + Bx - 15(0.6) \sum Fy = 0 = -25(0.8) + Cy +By + 15(0.8) \sum MB = 0 = 60 -25(0.8)(2.5) + Cy(5) +15(0.6)(1.5) Solving the equations we get Bx = 18.75 lb, By = 31.25 lb, and Cy = 31.25 lb

 

[wais]

Based on the information provided, it seems like you have set up the equations correctly. However, in order to solve for the initial vertical reaction at C and the horizontal and vertical components of reaction at B, you need to have three equations to solve for three unknowns. Right now, you only have two equations (sum of forces in the x and y directions). To find the third equation, you can use the moment equilibrium equation about point A. This will give you the third equation needed to solve for the three unknowns (By, Cy, and Bx).

To set up the moment equilibrium equation, you can choose any point along the bar AB. Let's choose point B. The moment equilibrium equation about point B would be:

\sum MB = 0 = -60 -25(0.8)(2.5) + By(5) -15(0.6)(1.5)

This equation should give you the third equation needed to solve for the three unknowns. Once you have all three equations, you can solve for By, Cy, and Bx using any method of your choice (substitution, elimination, etc.).

I hope this helps and good luck with your calculation!