Discussion Overview
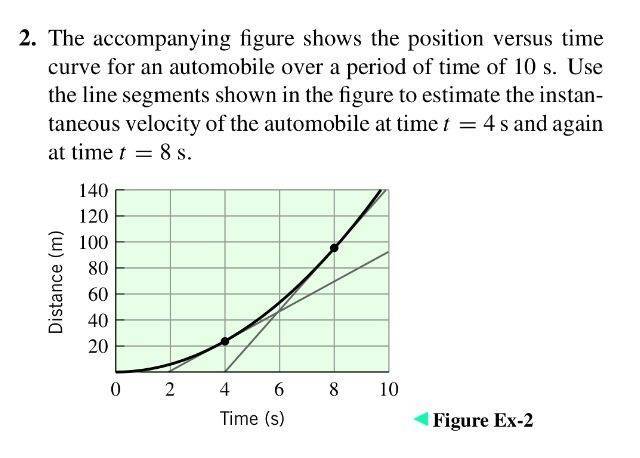
The discussion revolves around determining the instantaneous velocity at specific points on a graph, particularly at 4 seconds and 8 seconds. Participants explore the relationship between the tangent of a curve and its slope, which is linked to the concept of instantaneous velocity.
Discussion Character
- Technical explanation, Conceptual clarification, Homework-related
Main Points Raised
- One participant questions how to find instantaneous velocity using the tangent of the curve at given time points.
- Another participant confirms that the tangent represents the slope and equates slope to velocity, suggesting a method of counting squares on the graph.
- A later reply acknowledges the previous comments and expresses a light-hearted desire to delete their post, indicating a casual tone in the discussion.
- Further, another participant appreciates the input, suggesting that the discussion may be beneficial to others as well.
Areas of Agreement / Disagreement
Participants generally agree on the relationship between the tangent, slope, and velocity, but the method for calculating instantaneous velocity remains somewhat informal and not fully detailed.
Contextual Notes
The discussion does not delve into specific mathematical methods or definitions for calculating instantaneous velocity, leaving some assumptions and steps unresolved.