Determine the location of the subset

[mathlearn]

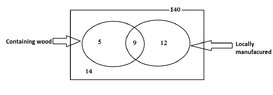
In a furniture store there are 40 types of furniture for sale. Among them 26 types are wood free and , out of the wood free types , 12 are locally manufactured.Furthermore, the number of locally manufactured types containing wood is 9

View attachment 5979

Problem

First I drew the relevant venn diagram.

ii.How many furniture types that contain wood are not manufactured locally? Done and updated the venn diagram

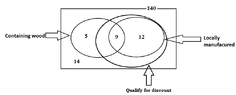
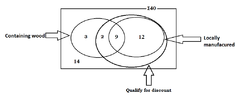
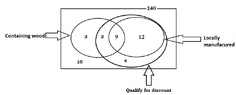
In this store , a discount is given to all locally manufactured types of furniture and to some types of furniture that are not manufactured locally. There are 11 types of furniture containing wood that qualify for discounts and there are 13 types of furniture that do not qualify for the discounts.

Where do i need help:

iii.In a copy of the venn daigram drawn in i above , draw a subset suitably to indicate the types of furniture that qualify for discounts , and include clearly all the given information in the copy.

I need help to determine the location of the subset.

Many Thanks :)

 

[MarkFL]

Okay, let's look at the statement:

In this store , a discount is given to all locally manufactured types of furniture and to some types of furniture that are not manufactured locally.

This means our new subset should include ALL of the locally manufactured and some of each of the other two types:

View attachment 5980

Now, let's look at:

There are 11 types of furniture containing wood that qualify for discounts...

So, we need to make the following change:

View attachment 5981

And finally, let's look at:

...and there are 13 types of furniture that do not qualify for the discounts.

Hence, we need:

View attachment 5982

Does that all make sense?

 

[mathlearn]

Thank you very much (Smile)