Further Understanding Simultaneity Conventions

[Freixas]

Summary

Almost a year ago, I created a post titled “Understanding the phrase 'simultaneity convention'”. The answers included requirements for defining a simultaneity convention. But some simultaneity conventions, while meeting all the requirements, still appear problematic. What am I missing?

Answers form my earlier post:

From @Dale: A coordinate chart is a mapping between events in spacetime and points in R4. There are very few requirements. The mapping must be smooth (diffeomorphic) and one-to-one (invertible). Other than that you are not restricted.

The simultaneity convention is then just the convention you used to choose which events share the same t coordinate. The usual implication is that the coordinate basis vector for t is timelike, but I am not certain even that is actually required.

From @PeterDonis: A spacetime is a 4-dimensional set of events. A "simultaneity convention" is a way of breaking up the spacetime into disjoint 3-dimensional subsets, such that all of the events in each subset are defined to happen "at the same time". This requires that, for each subset, all of the events in the subset are spacelike separated from each other (meaning that no two events can be connected by a timelike or null curve).

Given the above, the possible range of "simultaneity conventions" is obvious: any division of 4-dimensional spacetime into 3-dimensional subsets that meets the above requirements is a valid "simultaneity convention".

Discussion

I have tried searching for a good, layman's definition of a “coordinate chart” and failed. Most definitions read, to me, as gobbledygook. Here is my best guess as to what Dale said:

Spacetime as a collection of events. These events can be assigned coordinates using various systems; for example, Cartesian coordinates, polar coordinates, etc. Could a coordinate chart represent a choice of such a system? Even when we choose a system, we cannot assign coordinates to events without selecting an observer and a simultaneity convention.

If this guess is correct, then I can sort of follow Dale's answer, although it sounds as though a simultaneity convention could be any arbitrary method of assigned a time coordinate as long as the assignment is smooth and one-to-one. I'm not at all sure that my guess is correct.

Peter's answer seems similar, but written more for a layman. He has no diffeomorphic requirement, but I'll assume it's there. Peter adds the concept that within the set of all possible simultaneity conventions, some are valid and some are invalid. Dale noted elsewhere that the requirement Peter added is not universally required by all physicists.

The missing observer

We know that events that are simultaneous for one observer will not necessarily be simultaneous for another. Therefore, I would have thought that any definition of simultaneity would include “relative to an observer”. As I mentioned above, perhaps this is implied as part of the coordinate chart. It's not clear.

I would think that the if we wanted to preserve Einstein's first postulate, whatever simultaneity convention we chose would be the same relative to any observer—we wouldn't have one convention for one observer and a different one for another.

Simultaneity conventions and the one-way speed of light

Einstein establishes simultaneity by calculating how long a light pulse takes to travel a known distance. If a set of observers are at rest relative to each other, their clocks mark time at the same rate. If one observer sends a light pulse to the others at time 0, then the receiving observers can synchronize their clocks by setting it to the pulse's travel time.

If we choose a one-way speed of light in one direction, then we could apply Einstein's method to establish simultaneity, so the choice of a one-way speed defines a simultaneity convention. But the answers I was given approach the problem from the other end: given a convention, we could presumably calculate the one-way speed of light in a specific direction.

In another thread, I was told that the choice of the one-way speed of light was equivalent to choosing the mathematical system used to solve physics problems. Can we say the same if we instead choose a simultaneity convention?

In general, is the one-way speed of light the flip side of choosing a simultaneity convention?

Valid and invalid conventions

Dale's answer simply defines a simultaneity convention without qualifying them as “good”, “bad”, or even “useful”.

Peter introduced the idea that there are “valid” and “invalid” conventions. The restriction he mentioned seems to be widely accepted.

What objective criteria, if any, could be used to separate valid from invalid conventions. Or are all such criteria subjective?

Investigation

I hope I've clarified that I am not a mathematician. I would like to think that I can still do some analysis of simultaneity conventions.

If we specify a simultaneity conventions by selecting a constant one-way speed of light in one direction, then this can be represented geometrically on a standard Minkowski spacetime diagram by skewing the X axis by a given amount. I used this approach to create a geometrical method for analyzing a subset of all the possible conventions:

I began by picking a function of the form $f(x, T) = t$ which met all the following criteria:

• $f(0, T) = T$
• The mapping is invertible: Every $(x, T)$ maps to one and only one $(x, t)$.
• The mapping is diffeomorphic (“smooth”).
• Every pair of coordinates that share a common $T$ can be connected by a spacelike curve.

The selected function maps $(x, T)$ coordinates, coordinates using my simultaneity convention, to $(x, t)$ coordinates, coordinates using Einstein's simultaneity convention (a standard Minkowski spacetime diagram). I believe such a function allows me to define a simultaneity convention that meets all of Dale's and Peter's requirements. According to Peter, all such functions should define valid conventions.

By drawing a standard Minkowski $(x, t)$ diagram, choosing a specific $T$, and drawing the curve for $f(x, T) = t$, I can project a single line of simultaneity from $(x, T)$ space onto $(x, t)$ space. Because $f(0, T) = T = t$, I know this curve will cross the $t$ axis at the selected $T$ value. Drawing a number of these allows me to project a grid of simultaneity lines onto my Minkowski diagram.

A problematic mapping

Consider $$f(x, T) = \frac {(sin(T) sin(x))} {2} + T = t$$

Here is what the grid for this convention looks like when projected on a normal Minkowski spacetime diagram:

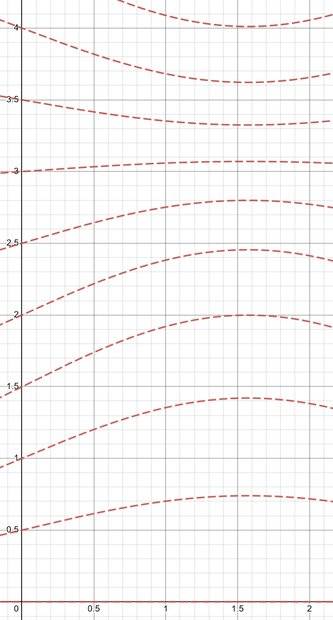With this convention, one cannot maintain clock synchronization among observers at rest in all cases. Since clocks move at the same rate for observers at rest, once two clocks are synchronized, they will remain synchronized. Logically, this should mean that, after synchronization, matching time values represent simultaneous times for those observers—but the convention says otherwise.

With this convention, it isn't clear that we can establish the one-way speed of light. Do we measure the speed along the main observer's lines of simultaneity for both departure and arrival? Or do we synchronize clocks for when the signal is sent and use the receiver's local time of arrival to determine the speed?

A convention which contradicts physics or creates ambiguities seems like a good candidate for an invalid simultaneity convention.

The convention I chose has other problems: it fails to obey Einstein's first postulate: the choice of an arbitrary 0 time coordinate is significant. Two observers, even with overlapping worldlines, may get different measurements for the one-way speed of the same photon if they choose different 0 time. In general, any convention that allows the one-way speed of light to vary creates unique inertial frames.

The argument for making these conventions invalid is weaker: unique inertial frames exist only within the context of the coordinate chart—there is no way to identify a unique inertial frame without choosing a system that makes that inertial frame unique. Making these conventions invalid is more an aesthetic choice—it keeps the physics cleaner by not implying properties that exist only within that convention.

Summary

Many physicists add a spacelike curve requirement to simultaneity conventions to maintain causality ordering. It looks to me as though there should be additional requirements, but I haven't heard of any others. Did I misunderstand something or is my analysis flawed?

 

[PeterDonis]

I have tried searching for a good, layman's definition of a “coordinate chart” and failed.

What's wrong with the definition @Dale gave you, explicitly, in what you quoted?

One of the reasons textbooks and lecture notes exist is to address these kinds of questions. Have you looked at, for example, Sean Carroll's online lecture notes on GR? (He also has a book containing an expanded version, but the online notes have the advantage of being free.)

The missing observer

The basic definition of simultaneity has nothing to do with "observers". You can overlay "observers" afterwards, but if you don't understand the basic underlying definition, trying to think about "observers" will only confuse you.

I would think that the if we wanted to preserve Einstein's first postulate, whatever simultaneity convention we chose would be the same relative to any observer—we wouldn't have one convention for one observer and a different one for another.

You have this backwards: the whole point of Einstein's first postulate is that the laws of physics are the same even though things like coordinate charts, reference frames, simultaneity conventions, etc., etc., etc., can be very different from one observer to another.

Peter introduced the idea that there are “valid” and “invalid” conventions.

You are quibbling about words. An "invalid" simultaneity convention is just something someone proposed that doesn't meet the given requirements. Which could equally well be expressed as it not being a simultaneity convention at all, because it doesn't meet the given requirements.

With this convention, one cannot maintain clock synchronization among observers at rest in all cases.

If you insist on Einstein clock synchronization (and if you are working in flat spacetime), then you have already specified a simultaneity convention: the one embodied in standard inertial frames and coordinate charts in SR. And of course this also means the one-way speed of light is isotropic.

Or, to turn this around, if you want to change clock synchronization, you must also change your simultaneity convention. The two go together. This should be obvious: "clock synchronization" is just a way of defining which different events happen at the same time. So is a simultaneity convention.

Many physicists add a spacelike curve requirement to simultaneity conventions

So did I, explicitly in what you quoted. The reason for the requirement is just what you say: causality. You don't want events that are causally connected to happen at the same time, i.e., to lie in the same simultaneity 3-surface.

 

[Dale]

Spacetime as a collection of events. These events can be assigned coordinates using various systems; for example, Cartesian coordinates, polar coordinates, etc. Could a coordinate chart represent a choice of such a system?

Yes.

Even when we choose a system, we cannot assign coordinates to events without selecting an observer and a simultaneity convention.

There is no requirement to select an observer. All you need is a mapping between the spacetime events and the coordinates. A simultaneity convention is an optional (but common) feature.

Dale noted elsewhere that the requirement Peter added is not universally required by all physicists.

That is correct, it is not universally required. But I also share @PeterDonis opinion on it. I think keeping the spacelike requirement is preferable.

In general, is the one-way speed of light the flip side of choosing a simultaneity convention?

Yes.

Consider f(x,T)=(sin(T)sin(x))2+T=t

Here is what the grid for this convention looks like when projected on a normal Minkowski spacetime diagram:

Excellent work! Yes, this looks valid to me.

Just a suggestion (not a correction): for organization I like to have my coordinate charts labeled with distinct symbols. So I would have the Minkowski coordinates $(t,x)$ and the new coordinates $(T,X)$. It is not necessary, what you did is fine, but it helps keep me organized. So then I would have the transformation equations $$t=\frac{\sin(X)\sin(T)}{2}+T$$$$x=X$$

With this convention, one cannot maintain clock synchronization among observers at rest in all cases.

That is correct. Some clocks at rest will be time dilated with respect to these coordinates. This is a (pseudo) gravitational time dilation (with reference to the equivalence principle).

it isn't clear that we can establish the one-way speed of light.

It will be spatially varying.

A convention which contradicts physics or creates ambiguities seems like a good candidate for an invalid simultaneity convention.

I haven’t done any of the math, but from your plots it doesn’t seem to present any contradictions or ambiguities.

The convention I chose has other problems: it fails to obey Einstein's first postulate:

Yes

Two observers, even with overlapping worldlines, may get different measurements for the one-way speed of the same photon if they choose different 0 time.

That would be a different coordinate chart with a different coordinate transform. We would not expect the same one way speeds.

Making these conventions invalid is more an aesthetic choice

Yes. You cannot really make them invalid, but you certainly can choose not to use them. You don’t need any particular justification for that aesthetic choice.

Did I misunderstand something or is my analysis flawed?

Your analysis seems fine. If you don’t like charts like your $(T,X)$ chart then you are not obligated to use them.

 

[Ibix]

A simultaneity convention and an origin implies a coordinate system, because you are able to assign four numbers uniquely to any event. However, a coordinate system does not necessarily imply a simultaneity convention, since it does not need to have coordinates that vary in a spacelike direction. An example is light one coordinates, where you take a Minkowskl diagram and rotate the grid 45°. The axes are null lines, so you have no implied simultaneity convention.

 

[vanhees71]

I think a very concise book about this is

E. Gourgoulhon, 3+1 formalism in general relativity, Springer (2012)

 

[Freixas]

Excellent work! Yes, this looks valid to me.

Thank you, Dale! And thanks for your detailed review.

That is correct. Some clocks at rest will be time dilated with respect to these coordinates. This is a (pseudo) gravitational time dilation (with reference to the equivalence principle).

Hmm. It sounds like this particular simultaneity convention requires entering into the world of GR. Within SR, once clocks at rest are synchronized, they should remain synchronized. The simultaneity convention I chose contradicts that, but apparently only within SR. Thanks for the clarification.

 

[Dale]

It sounds like this particular simultaneity convention requires entering into the world of GR.

No. This type of (pseudo) gravitational field is just a fictitious force. It shows up in ordinary Newtonian physics in non-inertial frames. In relativistic physics such pseudo forces also include time dilation.

General relativity is only required in the presence of tidal gravity which is spacetime curvature.

 

[Nugatory]

It sounds like this particular simultaneity convention requires entering into the world of GR.

Maybe better to say that it requires the mathematical methods of differential geometry because these are required to work with strange and unfriendly coordinate systems. In flat spacetime there's no reason to use such coordinates except, as here, to make a pedagogical point about coordinates in general but in GR we have no choice. From Sean Carroll's excellent quick intro to GR

The transition from flat to curved spacetime means that we will eventually be unable to
use Cartesian coordinates; in fact, some rather complicated coordinate systems become necessary. Therefore, for our own good, we want to make all of our equations coordinate
invariant...

... and we're off to an exposition of tensors. It might be somewhat interesting to write down the metric tensor as expressed in the coordinates of the initial post, verify that really does produce the correct results for the dot product of vectors expressed in those coordinates and that the Riemann tensor is still zero (use software for this calculation!).

 

[Freixas]

... and we're off to an exposition of tensors. But it might be somewhat interesting to write down the metric tensor as expressed in the coordinates of the initial post, verify that really does produce the correct results for the dot product of vectors expressed in those coordinates and that the Riemann tensor is still zero (use software for this calculation!).

LOL! You lost me at "tensors". I will leave this calculation to the experts. It would be interesting to see a discussion about this calculation and its results, but it is unlikely that I will be able to follow along. That let that hold anyone back--someone else might benefit.

 

[Nugatory]

LOL! You lost me at "tensors". I will leave this calculation to the experts. It would be interesting to see a discussion about this calculation and its results, but it is unlikely that I will be able to follow along. That let that hold anyone back--someone else might benefit.

Give grtiny.pdf a try anyways, it's a pretty low-stress introduction.

 

[Freixas]

There is no requirement to select an observer. All you need is a mapping between the spacetime events and the coordinates. A simultaneity convention is an optional (but common) feature.

You reminded me of a big source of confusion: is a coordinate chart a method for assigning coordinates to spacetime events ("Here are a set of rules. To create a mapping, follow the rules, which might include selecting an observer.") or is it the actual mapping?

It makes more sense to me as a method. For example, in solving a physics problem, I might have several observers, which would result in several possible coordinate systems. I would want all the coordinate systems based on the same rules, which could include a simultaneity convention. If a coordinate chart is the actual mapping, then I would need different charts for each observer, which would seem to introduce the possibility of mixing apples and oranges.

I must have read dozens of definitions of a coordinate chart and never got a clear answer to this question.

 

[Dale]

is a coordinate chart a method for assigning coordinates to spacetime events ("Here are a set of rules. To create a mapping, follow the rules, which might include selecting an observer.") or is it the actual mapping?

It is the actual mapping.

in solving a physics problem, I might have several observers, which would result in several possible coordinate systems

The idea of observers and coordinate systems becomes somewhat of a fetish in relativity teaching. Although it is ubiquitous, there is no need to associate a coordinate system with an observer nor is there any need for an observer to use a particular coordinate system.

In particular there is no need for an observer to use a coordinate system where they are at rest. I can go to the store, I don’t need to have the store come to me.

I must have read dozens of definitions of a coordinate chart and never got a clear answer to this question.

Well, I personally thought my definition was pretty clear on that point.

 

[Freixas]

Give grtiny.pdf a try anyways, it's a pretty low-stress introduction.

I'll give it a try. I like the intro statement "However, these statements are incomprehensible unless you sling the lingo." which sounds promising. A short skim further, though, and I see his clarifications still slinging an awful lot of lingo. :-)

 

[Nugatory]

“….To create a mapping, follow the rules, which might include selecting an observer”

”Select an observer” is how to say “Specify the origin of the coordinate system you’re choosing” without losing a math-averse audience. It’s not exactly wrong, but it tends to attach more physical significance ro coordinates than they merit.

 

[Freixas]

It is the actual mapping.

The idea of observers and coordinate systems becomes somewhat of a fetish in relativity teaching. Although it is ubiquitous, there is no need to associate a coordinate system with an observer nor is there any need for an observer to use a particular coordinate system.

In particular there is no need for an observer to use a coordinate system where they are at rest. I can go to the store, I don’t need to have the store come to me.

Well, I personally thought my definition was pretty clear on that point.

Here's where I got confused. You said "The simultaneity convention is then just the convention you used to choose which events share the same t coordinate." The step before this was to choose a coordinate chart.

If a coordinate chart is a mapping from spacetime to coordinates and if one chooses a coordinate chart that produces (x, y, z, t) coordinates, why would I need to choose which events share the same t coordinate? Hasn't the coordinate chart already done this? This statement introduced the possibility in my mind that a coordinate chart was a method rather than a final mapping.

 

[Dale]

Hasn't the coordinate chart already done this?

Yes. I am sorry about the confusion. “the convention you used to choose which events share the same t coordinate”. The word “used” in the past tense was intended to convey that this choice was already done. Specifically that it was already done as part of the choice of coordinates. The simultaneity convention is not something separate from your coordinates, it is just part of the coordinates.

 

[Freixas]

That is correct, it is not universally required. But I also share @PeterDonis opinion on it. I think keeping the spacelike requirement is preferable.

Long ago, I thought that the simultaneity of two events (relative to an observer) could be absolutely determined (i.e. that the speed of light was isotropic and that this was a fact and not just one of may possible choices). Then I learned about how Einstein had decided, by definition, that the speed of light was isotropic, and I switched to thinking that simultaneity was just an arbitrary construct--any two events could be simultaneous given the right choice for a simultaneity convention.

A bit more thinking and I realized that there is one case where simultaneity is an invariant: when two events occur in the same place at the same time. I also realized that two events at different times along one's worldline could never be simultaneous (to oneself). And I also learned that physicists didn't really like to consider events connected by timelike (or lightlike) curves to be simultaneous.

I was considering how I might introduce some of these concepts to friends who are neither mathematicians or physicists. In the process of creating a simple example, it occurred to me that there might be some limits we could impose on simultaneity.

Let's say I have a dog. I leave the dog at home and go to work. When I return, I discover that my dog has escaped. The dog's escape has to be simultaneous with some event on my worldline between the time I left and the time I returned. Any simultaneity convention in which this is not true might fit a mathematical definition of a simultaneity convention, but would seem to violate any real world concept of simultaneity.

Why? Well, I tried to picture how I would explain to a lay person that this was not true, and I couldn't think of an explanation that would make any sense. My wordline and my home's worldline separated and rejoined. Events occurring at the same time when our worldlines are joined are simultaneous in the strongest sent (invariant). Whatever the simultaneity correspondence of the events that occurred while the worldlines separated might be, every event on my worldline must have a correspondence on my home's worldline, even if I can't say which events correspond.

Thinking further, I came up with a scenario in which I did not have to be home at all. I'm at work. I call my wife at home and leave a message. Later, she calls me and tells me that she received my message and that, sometime after hearing it, the dog escaped. At least one event on my worldline from the time I left the message to the time I received my wife's call must be simultaneous with the escape of the dog.

Formalizing this, I send a light pulse to some distant location, where it is reflected back to me. The event corresponding to the reflection of the pulse must be simultaneous to some event on my worldline from the time I sent the pulse to the time I received the reflection.

Any simultaneity convention in which this is not true would seem to violate our concept of simultaneity. I sketched out a diagram of the situation. It appears to me that any such convention would have timelike curves between events.

The usual argument is that conventions with timelike curves between simultaneous events can make events on some observer's worldline simultaneously. This has always seemed to me like a weak objection since we are only talking about coordinates assigned by one observer for another observer's worldline. The observer on whose worldline these events occur would not perceive the events as simultaneous.

As a causality problem, the only rule one has to maintain is that no observer can observer an effect before its cause. Conventions with timelike curves between events don't violate this.

The argument that I've presented here seems much stronger--the conventions violate our standard concept of simultaneity. (Try telling someone that their dog's escape did not occur sometime between their departure and return.)

My approach here does not apply to events connected by lightlike curves. however.

Since this is different from I usually hear, I suspect there must be a flaw in my assumptions, as I would be very surprised if any of this was novel. Maybe physicists like the usual argument because it is easier to state?

 

[Sagittarius A-Star]

Formalizing this, I send a light pulse to some distant location, where it is reflected back to me. The event corresponding to the reflection of the pulse must be simultaneous to some event on my worldline from the time I sent the pulse to the time I received the reflection.

That's the "spacelike requirement". You see this, when you draw the light cone for the reflection event. I don't understand, what your problem is.

 

[Nugatory]

there is one case where simultaneity is an invariant: when two events occur in the same place at the same time.

That's a single event - there's no such thing as two events happening at the same time and place. An event is defined as a single point in spacetime, no matter how many interesting things are going on at that point. (This is one of many examples of physics terms that don't mean what they do in natural language).

I also realized that two events at different times along one's worldline could never be simultaneous (to oneself). And I also learned that physicists didn't really like to consider events connected by timelike (or lightlike) curves to be simultaneous.

"Simultaneous" means "has the same time coordinate" and that concept is only defined when using coordinate systems that have certain properties (loosely speaking, the ones we use naturally: inertial and non-perverse with one timelike and three spacelike orthogonal axes - I'm asking for a generous interpretation of "loosely" here). If you are using such a coordinate system then
a) Two events at different times along one's worldline can never be simultaneous, and the "to oneself" qualifier is unnecessary - the statement is true for all such coordinate systems.
b) It's not that physicists "don't like" to consider events separated by timelike or lightlike curves to be simultaneous - it is mathematically impossible for such events to have the same time coordinate when using non-perverse coordinates.
Conversely, if your coordinate system doesn't have the necessary properties then it doesn't support a notion of simultaneity, and we fall back on the more general and invariant notions of spacelike, timelike, and lightlike separation.

The dog's escape has to be simultaneous with some event on my worldline between the time I left and the time I returned. Any simultaneity convention in which this is not true might fit a mathematical definition of a simultaneity convention, but would seem to violate any real world concept of simultaneity.

I would rather say that the such a coordinate system doesn't have any notion of simultaneity.

every event on my worldline must have a correspondence on my home's worldline, even if I can't say which events correspond.

Sure, and that correspondence is "has the same time coordinate". All such mappings (using non-perverse coordinates) will be between spacelike separated events - the events on your worldline which might be defined to be simultaneous with the dog's escape will be exactly the ones that are spacelike/lightlike separated from the escape event (these are a subset of the events on your worldline between your departure and your return). That's the common thread in your subsequent refinements of the example.

Since this is different from I usually hear, I suspect there must be a flaw in my assumptions, as I would be very surprised if any of this was novel. Maybe physicists like the usual argument because it is easier to state?

It's more that the simultaneity mapping between two spacelike separated events isn't especially useful. What would be useful is be for the event "dog escapes" to be in the future lightcone of the event "Oops, remembered I left the gate open, better call my wife".

 

[Freixas]

That's the "spacelike requirement". You see this, when you draw the light cone for the reflection event. I don't understand, what your problem is.

My statement "The event corresponding to the reflection of the pulse must be simultaneous to some event on my worldline from the time I sent the pulse to the time I received the reflection," implies that there must be at least one event on my worldline that is spacelike or lightlike connected to the reflection event.

In any case, what I am trying to say (right or wrong) is that , in this case, any simultaneity convention in which no events on my worldline are spacelike or lightlike connected to the reflection event violates my concept of simultaneity (and my concept may also be wrong).

 

[Sagittarius A-Star]

My statement "The event corresponding to the reflection of the pulse must be simultaneous to some event on my worldline from the time I sent the pulse to the time I received the reflection," implies that there must be at least one event on my worldline that is spacelike or lightlike connected to the reflection event.

As @Nugatory said, the condition for defined simultaneity is a spacelike (not light-like) separation when using non-perverse coordinates.

 

[Freixas]

That's a single event - there's no such thing as two events happening at the same time and place. An event is defined as a single point in spacetime, no matter how many interesting things are going on at that point. (This is one of many examples of physics terms that don't mean what they do in natural language).

Here's a quote for Einstein's SR paper: "We have to take into account that all our judgments in which time plays a part are always judgments of simultaneous events. If, for instance, I say, “That train arrives here at 7 o’clock,” I mean something like this: “The pointing of the small hand of my watch to 7 and the arrival of the train are simultaneous events.” Here, Einstein uses the plural "events" for two things that happen at the same time and place.

The definitions have probably been tightened since 1905, so point taken.

a) Two events at different times along one's worldline can never be simultaneous, and the "to oneself" qualifier is unnecessary - the statement is true for all such coordinate systems.
b) It's not that physicists "don't like" to consider events separated by timelike or lightlike curves to be simultaneous - it is mathematically impossible for such events to have the same time coordinate when using non-perverse coordinates.

Here's what I hear: non-perverse coordinates are defined to be coordinates that meet certain conditions and therefore, any coordinates that don't meet those conditions are perverse. This is a tautology. I mean, you may have a valid point, but your definition of "perverse" is vague.

In the previous discussion on simultaneity conventions (see link in the OP), Dale mentioned that not all physicists agree that simultaneity conventions are restricted to those where events are only connected by spacelike curves. He repeats the point here in comment #3, so it sounds as though your viewpoint is not universal even among physicists.

I would rather say that the such a coordinate system doesn't have any notion of simultaneity.

Dale gave what I'm calling a mathematical definition of simultaneity conventions (see OP). Using his definition, one could define a convention (coordinate system) in which none of the events in my worldline is simultaneous with the dog's escape. These events would still be simultaneous with whatever other events have the same time coordinate, so there would be, in fact, a notion of simultaneity.

Sure, and that correspondence is "has the same time coordinate". All such mappings (using non-perverse coordinates) will be between spacelike separated events - the events on your worldline which might be defined to be simultaneous with the dog's escape will be exactly the ones that are spacelike/lightlike separated from the escape event (these are a subset of the events on your worldline between your departure and your return). That's the common thread in your subsequent refinements of the example.

We seem to be in closer agreement here, except that I would leave out the "using the non-perverse coordinates". But what I'm saying is just slightly different.

Let's use the light reflection example. What I'm saying is that the normal concept of simultaneity is one in which at least one event on my worldline between emission and reception is simultaneous with the reflection event. This event would then have to be either spacelike or lightlike connected to the reflection event. I'm not saying that such a convention only has spacelike/lightlike connections with other events with the same time coordinate, although I suspect that a proof is possible that shows that this is also true.

For what it's worth, I'm told physicist don't like simultaneous events being connected with lightlike curves any more than with timelike ones.

It's more that the simultaneity mapping between two spacelike separated events isn't especially useful. What would be useful is be for the event "dog escapes" to be in the future lightcone of the event "Oops, remembered I left the gate open, better call my wife".

I've been hanging out in the forum long enough that I think I actually know what you're getting at. But I started out by thinking about how I might explain this lack of usefulness of simultaneity to lay people. That led me to think that even though I can't declare any two events to be simultaneous in any absolute way, I might be able to put some bounds on which events might be simultaneous based on how people think about simultaneity.

If I leave home and return to find my dog escaped, people would normally accept that the escape happened sometime during the time I was away. It would be incomprehensible for the dog to have escaped before I left or after I arrived, given that the dog was present when I left and missing when I returned. I then generalized this idea to the reflection example. This seems to me to be a clearer argument for making simultaneity conventions with timelike events invalid.

The usual argument against timelike curves connecting simultaneous events is harder for me to follow. Here's what that argument sounds like to me: "You can't have two events on any worldline be simultaneous." "Why?" "Because they can't." "Why?" "Because they are different events." "So?" "Well, you can't toss a ball and catch it at the same time, right?" "No one is tossing a ball and catching it at the same time--someone else has just assigned the same time coordinate to the two events. The person tossing and catching would not use these coordinates. In fact, even the person who assigned the coordinates will never actually observe the toss and the catch happening simultaneously--they only calculate these to be simultaneous events based on their coordinate system choice."

 

[Freixas]

As @Nugatory said, the condition for defined simultaneity is a spacelike (not light-like) separation when using non-perverse coordinates.

Maybe I need a clearer definition of perverse and non-perverse.

My own argument may be making a case that timelike simultaneity is "perverse" in the sense of a lay person's idea of simultaneity. I'll repeat the example of "perversion" I just used in my reply to Nugatory: "If I leave home and return to find my dog escaped, people would normally accept that the escape happened sometime during the time I was away. It would be incomprehensible for the dog to have escaped before I left or after I arrived, given that the dog was present when I left and missing when I returned."

Unfortunately, when generalized to the example where I bounce a light pulse, I can't exclude lightlike simultaneity without a priori defining it to be forbidden. I could disallow light traveling instantaneously in one direction, which would solve the problem, but would introduce the question "Why?" When I asked in a previous discussion, the answer was that you can't have emission and reception be simultaneous, which sounds like a circular argument.

I'm not saying there isn't a good argument. I'm just saying I haven't heard it.

 

[Ibix]

But I started out by thinking about how I might explain this lack of usefulness of simultaneity to lay people. That led me to think that even though I can't declare any two events to be simultaneous in any absolute way, I might be able to put some bounds on which events might be simultaneous based on how people think about simultaneity.

I think the easiest layman-friendly way to think about it is to say that in pre-relativistic physics you can define "the future", which is all the things that you could (in principle) affect some way, and you can define "the past" which is all the things that could (in principle) have already affected you now in some way. There's a slightly shaky instant in the middle called "the present" where it isn't entirely clear if you can affect or be affected by things happening now.

Relativity retains the same concepts of "the future" and "the past", but adds that causal influences cannot propagate faster than light. That means that "the present" is no longer defineable as "the boundary between past and future" because there's quite a big gap between past and future - one light second away from you there's a two second gap between the events you'd call "in the past" and "in the future". Also, it makes past, present and future explicitly personal concepts. My past is my past lightcone and its interior; yours is your past light cone and its interior, and they are not quite the same thing. And my present is the event I'm at now and yours is the event you are at now and they are not the same thing.

That "gap" between the past and future is actually really important. It gets rid of the haziness over whether something happening in the present can affect you or not - no it can't, unless it's at the same event. And it also takes away any physical meaning for "the present", so you're free to define it (or not define it at all) as long as whatever arbitrary line you draw dividing past from future never enters the past or future light cone of any event through which it passes - including your own personal "now".

You can even explain why none of this is relevant to every day life - which is that even for something a few kilometers away the "gap" between past and future is measured in milliseconds, so you just don't notice it.

 

[PeterDonis]

Maybe I need a clearer definition of perverse and non-perverse.

I already gave it to you, way back in post #2: you don't want events that are causally connected to be simultaneous. The events of emission and reception of a light ray are causally connected, so in any non-perverse coordinates they will not be simultaneous.

 

[Dale]

A bit more thinking and I realized that there is one case where simultaneity is an invariant: when two events occur in the same place at the same time

Yes. In this case the two events are actually one event. An event is always simultaneous with itself.

I tried to picture how I would explain to a lay person that this was not true, and I couldn't think of an explanation that would make any sense.

So, if we include the common restriction that surfaces of simultaneity (constant $t$ coordinate) must be spacelike, then we can easily show that along any timelike worldline $t$ is strictly increasing. Otherwise two timelike separated events would share the same $t$ coordinate, which violates the restriction. Since $t$ is strictly increasing, that immediately implies that $t_{work}<t_{escape}<t_{home}$.

 

[Freixas]

I think the easiest layman-friendly way to think about it is to say...

Thanks!

 

[Freixas]

I already gave it to you, way back in post #2: you don't want events that are causally connected to be simultaneous. The events of emission and reception of a light ray are causally connected, so in any non-perverse coordinates they will not be simultaneous.

Yes, I heard you. It's just not clear why this is something I "don't want". I hate to sound obtuse. My alternatives were to ignore you or to lie and say I totally get it.

I have to think about Dale's response #26 and see if he is actually explaining the restriction in a way that makes sense. My post #17 is a way to try to get to the same point from a different direction. It's not a complete argument and Dale's response might or might not be the final piece.

By the way, are "perverse" and "non-perverse" coordinates an actual thing with a precise definition or is it just a term that @Nugatory invented?

 

[Nugatory]

By the way, are "perverse" and "non-perverse" coordinates an actual thing with a precise definition or is it just a term that @Nugatory invented?

It's not original with me, I think I first heard it from an assistant professor back in my undergraduate years.
It seemed a reasonable enough term to apply to a choice of coordinates that makes a problem harder to understand or obscures the physics.

It's just not clear why this [events that are causally connected to be simultaneous] is something I "don't want".

That would mean that the cause and the effect have the same time coordinate even though they are spatially separated, and therefore that the effect is propagating with an infinite coordinate speed. That will definitely get in the way of understanding the physics at work in this interaction. @PeterDonis says "definitely don't want that", I say choosing that would be "perverse".

 

[PeterDonis]

we can easily show that along any timelike worldline is strictly increasing

Or any null worldline. The condition that simultaneity surfaces must be spacelike prevents any pair of events that are not spacelike separated from having the same $t$ coordinate.

 

[PeterDonis]

It's just not clear why this is something I "don't want".

Causality implies ordering: one event is the "cause" and the other is the "effect", and the latter comes after the former. But "simultaneous" implies "at the same time", i.e., neither event comes before the other. So any coordinate chart that allows causally connected events to be simultaneous would seem to be perverse because the coordinates do not respect the ordering of causally connected events.

 

[PeterDonis]

I hate to sound obtuse. My alternatives were to ignore you or to lie and say I totally get it.

You left out a third alternative: ask. Asking doesn't make you sound obtuse. It makes you sound like someone who is actually paying attention to what other people post. That's a good thing.

 

[PeterDonis]

I have to think about Dale's response #26

He is saying the same thing I said in post #31 (and in post #30 I added the fact that what he said applies to null as well as timelike worldlines--i.e., to all causal curves), just in different words. Basically the idea is that any non-perverse coordinate chart should have its timelike coordinate (which @Dale called $t$) strictly increasing along any causal curve.

 

[Dale]

Or any null worldline. The condition that simultaneity surfaces must be spacelike prevents any pair of events that are not spacelike separated from having the same $t$ coordinate.

Yes, good point.

 

[vanhees71]

My statement "The event corresponding to the reflection of the pulse must be simultaneous to some event on my worldline from the time I sent the pulse to the time I received the reflection," implies that there must be at least one event on my worldline that is spacelike or lightlike connected to the reflection event.

Of course it is. Just draw a Minkowski diagram. The observer's world line is the $x^0=ct$ axis. Then you draw in parallel the world-line of the mirror at some distance $L$ and the light cone depicting the phase of the electromagnetic wave being reflected on the mirror. Then it's very clear at which (coordinate) time the reflection occurs.

It's of course clear that the Minkowski diagram is constructed from Einstein's synchronization convention, assuming all the symmetries of Minkowski space, i.e., that there must be a description of the inertial frame, where space occurs as a Euclidean 3D affine manifold for an observer at rest relative to this inertial frame. One should be aware that there's no a-priori definition of a "one-way speed of light" since you can only measure coincidences between spacetime points, and that's why you need the mirror to measure the time of the light signal with one clock at the place of the observer. Then the isotropy of space is used to define the synchronized clock at the place of the mirror to assume that the time the light signal needs to reach the mirror is the same as the time the reflected signal needs to go back to the observer, and this is done by convention for observer and mirror at rest relative to each other.

This defines the Minkowski diagram, including the measure of space-time units (Lorentzian coordinates). The same construction must be done for any inertial frame, which determines also the space-time units for this other frame, moving with constant velocity wrt. the first one.

You can short-cut this rather involved construction by first introducing the Minkowskian space-time geometry as an affine pseudo-Euclidean manifold with Lorentz-signature fundmamental form, which leads (in the usual (1+1)-dimensional Minkowski diagrams) to the time- and space-like unit hyperbolae defining the "tic marks" on the space-time axes of different inertial reference frames (together with the light cones, which must always be bisectors of the angle between space and time axes of the inertial frame (when using the usual convention to measure $c t$ on the time-like axes).

In any case, what I am trying to say (right or wrong) is that , in this case, any simultaneity convention in which no events on my worldline are spacelike or lightlike connected to the reflection event violates my concept of simultaneity (and my concept may also be wrong).

Of course, two events that are simultaneous in some inertial frame must be space-like separated in any other inertial frame too. After all the property of vectors being space-like, light-like, or time-like are invariant properties, defined by the Minkowski product between these vectors.