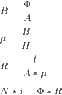Determine the shunt field current in a magnetic circuit

[Fatima Hasan]

Homework Statement

Written below.

Relevant Equations

Equations are attached below.

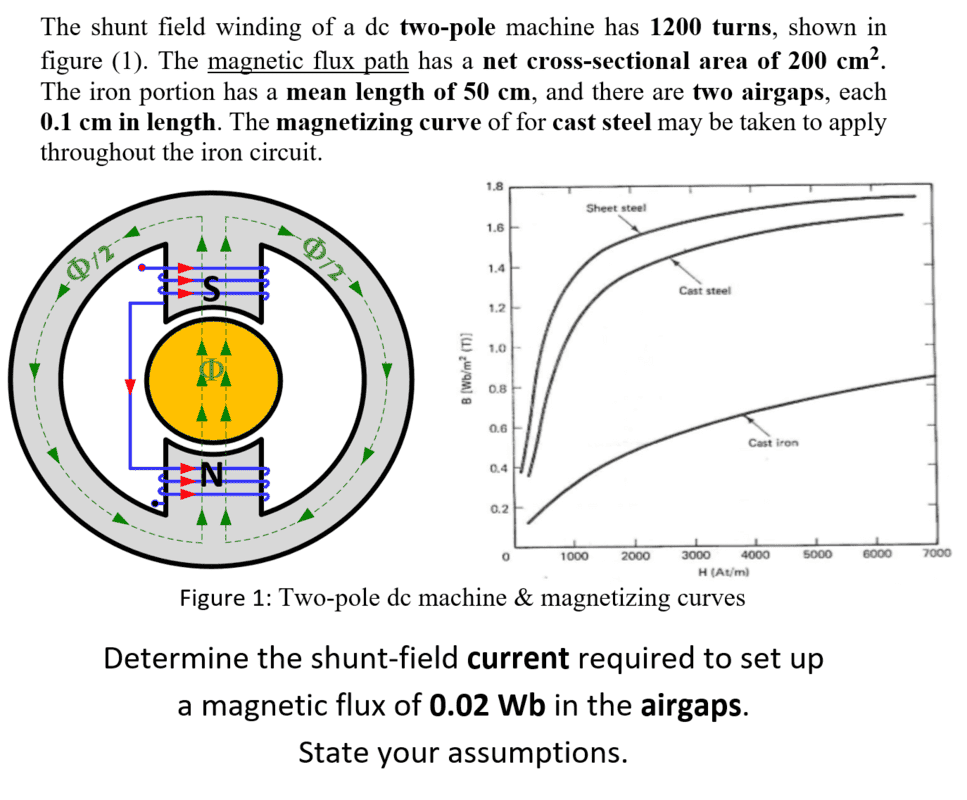
Problem Statement :

Here's my attempt :
* By assuming that the fringing and leakage effects are ignored.

I find the flux density , the permeability and the reluctance of the iron , but then I get stuck .
Any help would be greatly appreciated .

 

[Fatima Hasan]

I tried to solve it , and that's what I got :
Analog Circuit :

That's what I got , but I am not sure if my answer is correct or not .
I want to confirm my answer .

 

[alan123hk]

The statement states that the flux path has a net cross-sectional area of 200 cm^2.
Based on this statement, I am a bit confused about the assumption that the cross-sectional area of left branch and right branch of the toroidal core are the same as the cross-sectional area of the air gaps.

 

[rude man]

The statement states that the flux path has a net cross-sectional area of 200 cm^2.
Based on this statement, I am a bit confused about the assumption that the cross-sectional area of left branch and right branch of the toroidal core are the same as the cross-sectional area of the air gaps.

Yes it's not given. So I would assume the cross-section is uniform thruout the magnetic path, the drawing strongly suggesting otherwise notwithstanding.

 

[Babadag]

I agree with alan123hk: the "path" has to be the area for indicated path. That means the pole area has to be double=400 cm^2
Then n*I=Hfe*Lfe+B/μo*2*airgaplengs [n=number of turns]

 

[alan123hk]

Case 1 : the area is uniform throughout the magnetic path
Case 2 : the area of the pole is twice that of the left/right branch

Assume that the entire magnetic circuit has the same BH curve characteristics

In case 1, the B in the pole is twice that of the B in the left/right branch, and since the pole becomes bottleneck, the maximum magnetic flux density in the left/right branch may not be fully utilized.

In case 2, the entire magnetic circuit has the same B everywhere, there is no bottleneck, and the maximum magnetic flux density can be achieved throughout the entire magnetic circuit.

Of course, if uniform magnetic flux density is not the primary concern, then case 1 is still the choice in practical applications, since there may be many other factors to be considered, such as mechanical strength and reducing eddy current/hysteresis loss.