Guillem_dlc
- 188
- 17
Summary:: I'm solving an exercise.
I have the following center of gravity problem:
Having the function Y(x)=96,4*x(100-x) cm, where X is the horizontal axis and Y is the vertical axis, ranged between the interval (0, 93,7) cm. Determine:
a) Area bounded by this function, axis X and the line X=93,7 (in cm2)
b) The bar{x} coordinate of its centroid (in cm)
c) The bar{y} coordinate of its centroid (in cm)
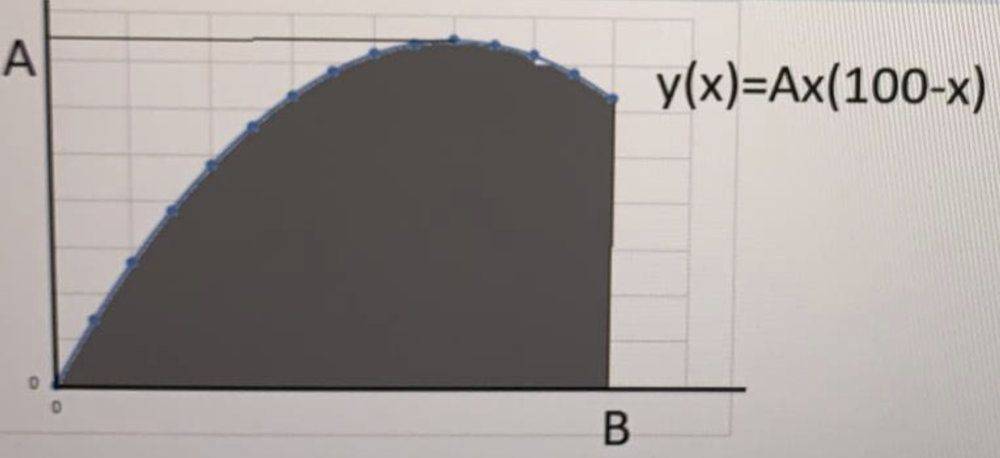
My attempt at resolution:

How can I calculate the last section if I can't clear the x?
Thanks!
I have the following center of gravity problem:
Having the function Y(x)=96,4*x(100-x) cm, where X is the horizontal axis and Y is the vertical axis, ranged between the interval (0, 93,7) cm. Determine:
a) Area bounded by this function, axis X and the line X=93,7 (in cm2)
b) The bar{x} coordinate of its centroid (in cm)
c) The bar{y} coordinate of its centroid (in cm)
My attempt at resolution:
How can I calculate the last section if I can't clear the x?
Thanks!