Determining equations for tension in 3D statics problem.

[VS9]

Homework Statement

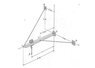
The steel beam is supported by cables AB and CD and a ball-and-socket joint at O. The position of the vertical point load, P influences the reaction at O as well as the tension in each cable.
First you need to derive the equations for the tension in cable AB, the tension in cable CD and the reaction at O in terms of x, which represents the placement of the point load, P, measured from the axis origin, point O.

We are given length of the beam and distances between things, but no other numbers.
The end goal is to put the three derived equations in a for loop for various values of x MATLAB.

Homework Equations

\Sigma F = 0
\Sigma M = 0

The Attempt at a Solution

I know how to solve problems using summation of forces and moments for problems where we must find forces acting on things, but I don't know how to set up a basic equation for tension in 3 dimensions.

I'm assuming I must set up vectors for the direction of the tensions, but am not exactly sure how to for this problem.

For example the direction vector of AB is r_AB= r_B-r_A=-6i+2j+3k, and the unit vector is
λ_AB=-6/7i+2/7j+3/7k with i, j, k being the vectors corresponding to x, y, and z.

If this is correct then the unit vector for CD should be λ_AB=-3/5i+4/5j

Where do I go from here? I'm thinking I need to make one force equilibrium equation for everything in the system, but I don't know how I would split that up into several equations.https://www.physicsforums.com/attachments/89824 https://www.physicsforums.com/attachments/89824

 

[robphy]

A Tension is a pull along the direction the [ideal] rope.
So, if you know their directions (from the relevant unit vectors), the missing pieces are the unknown magnitudes of those tensions (which are coefficients of those unit-vectors).

 

[VS9]

A Tension is a pull along the direction the [ideal] rope.
So, if you know their directions (from the relevant unit vectors), the missing pieces are the unknown magnitudes of those tensions (which are coefficients of those unit-vectors).

So if I find the unit vector for CD, do I just add the coefficients of i and j together to make a force equilibrium equation?

The unit vector for CD should be λ_AB=-3/5i+4/5j, correct?