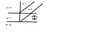Violagirl
- 112
- 0
Homework Statement
You decide to become a forensic pathologist because you enjoy working with dead people-they don't talk back-more than with the living. In one murder investigation, you find an unknown liquid in the victim's stomach. To identify this liquid, you pour a known amount of it onto a glass slide, such that it forms a film of thickness 500 nm on the side (with air above it). After doing this, you notice that, when illuminated with white light at normal incidence, light of wavelengths 500 nm and 700 nm is predominant in the reflected light (constructive interference). A) Determine the index of refraction for this liquid assuming the index of refraction of the glass slide is less than that of the liquid. B) What wavelengths of light in the visible spectrum range (400 - 700 nm) would have been observed if the index of refraction for the glass slide had been greater than the index found in part a for the unknown liquid? Hint: The observation of different wavelengths may correspond to different orders (differences in m) of the interference pattern for the different wavelengths.
Homework Equations
constructive interference:
δtot = 2m∏
λn2 = λ/n2
See attached diagram of situation.
The Attempt at a Solution
I definitely found this problem tricky. I would love to work through it with someone to better understand for my final this Saturday. Any help with it is appreciated. I have what I've been able to work out so far shown below and on the diagram attached.
δ1 = ∏
δ2 = (2d/λn2)2∏ <----- (Does this 2∏ reflect that it travels a full wavelength distance? Meaning that it shifts half a wavelength (pi) upon hitting the second medium. And since we're told that n3 is less than n2, it does not undergo a second inversion. So this would make sense for why constructive interference takes place but does the 2pi just correspond to the full wave length that is traveled?)
δtot = δ2 - δ1 = (2d/λn2) 2∏ - ∏
= 4d∏/λn2 -∏ = 2m∏
= 4d/λn2 -1 = 2m
= 4dn2/λ = 2m + 1
This is about as far as I could work out the problem. I'm not sure I understand what to do with the wavelength values provided. I know we have to solve for n2 but the hint about differences in m with wavelength did not make sense to me. Any help is appreciated.