BiggestAfrica
- 10
- 1
- Homework Statement
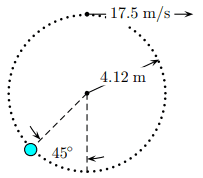
- A 4.1 kg ball is spun on a thin cord in a vertical circle having 4.12 m radius. It has a speed of 17.5 m/s at the highest point of the circle. Take zero potential energy at the lowest point and use the 45 degree angle measured with respect to the vertical as shown. The acceleration of gravity is 9.8 m/s^2.
Calculate the speed of the ball at angle 45 degrees.
- Relevant Equations
- Ko = Kf + Uf
.5(m)(vo^2) = (.5)(m)(vf^2) + mgh
I first found the height of the ball after it's passed the 45 degree angle by doing 4.12*sin(45) = 2.9133, and plugged in the rest of the variables (masses cancel)
.5(m)(vo^2) = (.5)(m)(vf^2) + mgh
(17.5^2)(.5) = (.5)(vf^2)(9.8*2.9133)
vf = 15.7845, however this is incorrect
I don't understand where I'm going wrong, so any help would be greatly appreciated!
.5(m)(vo^2) = (.5)(m)(vf^2) + mgh
(17.5^2)(.5) = (.5)(vf^2)(9.8*2.9133)
vf = 15.7845, however this is incorrect
I don't understand where I'm going wrong, so any help would be greatly appreciated!