Determining the Handedness of Circular Polarized Waves

[mrshappy0]

Homework Statement

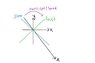
A polarized wave in the y axis, propagates in the z axis and is incident to a quarter-wave plate. Viewing the down from -z to z, the fast axis is 45deg below the x-axis.

Determine the polarization of the beam immediately following the quart-wave plate.

Homework Equations

Conceptual Question, I am not using equations..

The Attempt at a Solution

The wave must be circular but I cannot visualize how to determine whether it is left handed or right handed. I realize that if you curl your fingers in the direction that it rotates, the hand with the thumb pointing in the direction of propagation is the handedness but I can't visualize how the wave curls coming out.

 

[mrshappy0]

Haven't seen any replies yet so I am curious if there are any issues with this post.

 

[mrshappy0]

Well, I thought about it as I drifted off to sleep last night and I was thinking that crossing from from the slow axis (which must be orthogonal in this case) to the fast axis with the left hand allows for the thumb to be pointed in the direction of propagation. By doing this, I get a left handed curl. Is this correct? So in this case, it doesn't matter where the wave is polarized, as long as it has a non-zero component for the fast axis and a non-zero component for the slow axis, right??

Here is the image I drew for what I am doing.

 

[mrshappy0]

I believe if you were to apply the image above to the problem I posted, the fast and slow axis must be switched giving a right handed circle, I think.