STENDEC
- 21
- 0
I have a grid and want to determine whether a point lies within (our outside of) a circle.
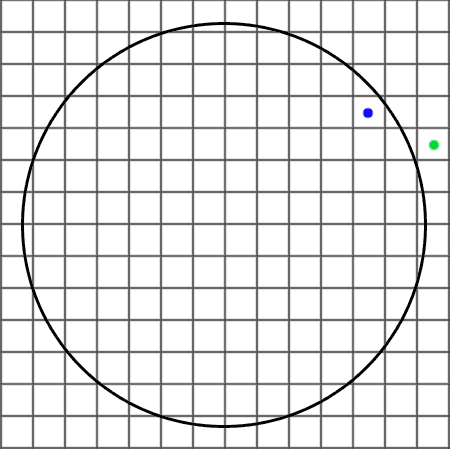
The grid cells simply have integer coordinates, e.g. x = 5, y = 7. The circle's radius is known, and also an integer value.
I wrote a program that can place points in a (quantized) circle using sin/cos, but I can't seem to wrap my head around how to check whether a grid cell lies within a circle of a given radius. Maybe someone can guide me into the right direction. Thanks.
The grid cells simply have integer coordinates, e.g. x = 5, y = 7. The circle's radius is known, and also an integer value.
I wrote a program that can place points in a (quantized) circle using sin/cos, but I can't seem to wrap my head around how to check whether a grid cell lies within a circle of a given radius. Maybe someone can guide me into the right direction. Thanks.