Cocoleia
- 293
- 4
- Homework Statement
- Diagonalize using creation / annihilation operator methods
- Relevant Equations
- a = 1/sqrt2 (y+dy)
a- = 1/sqrt2(y-dy)
I am given this Hamiltonian:
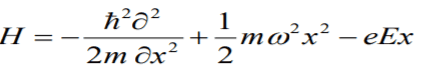
And asked to diagonalize.
I understand how we do such a Hamiltonian:
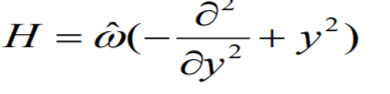
But I don't understand how to deal with the extra term in my given Hamiltonian. Usually we use
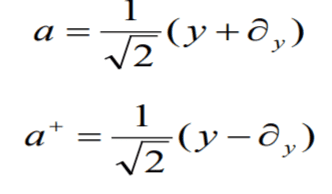
To get
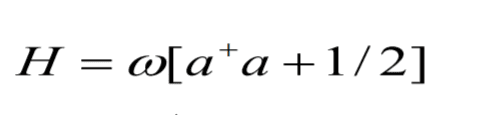
And asked to diagonalize.
I understand how we do such a Hamiltonian:
But I don't understand how to deal with the extra term in my given Hamiltonian. Usually we use
To get