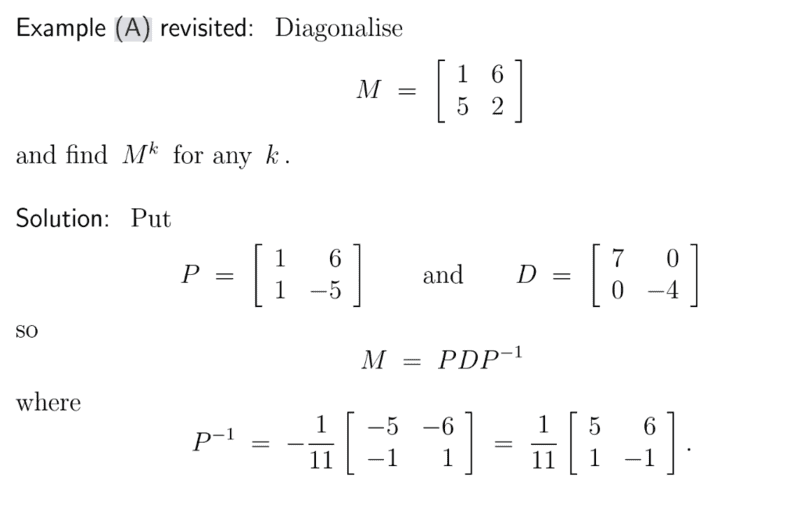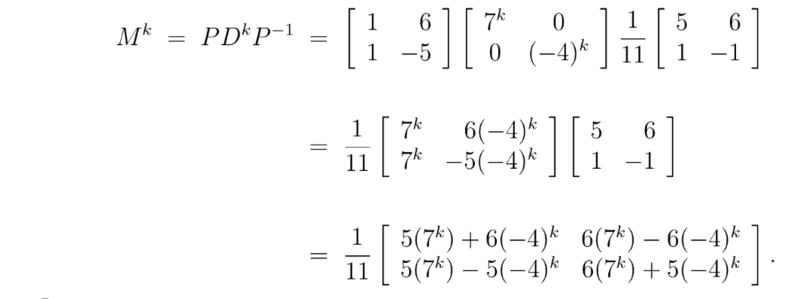SUMMARY
The discussion focuses on the process of diagonalizing a matrix, specifically addressing the derivation of matrices P and D from the eigenvalues of matrix M. The eigenvalues are determined by solving the equation ##\det(M-xI)=(1-x)\cdot (2-x) -5\cdot 6=0##. The Gauss-Jordan algorithm is recommended for solving the linear equation system ##PM=DP##, with the final expression for raising the matrix to the power k being ##M^k=(PDP^{-1})^k=PD^kP^{-1}##. The conversation also highlights the importance of recognizing cancellations in the matrix multiplication process.
PREREQUISITES
- Understanding of eigenvalues and eigenvectors
- Familiarity with matrix operations and properties
- Knowledge of the Gauss-Jordan elimination method
- Basic concepts of linear algebra
NEXT STEPS
- Study the process of finding eigenvalues and eigenvectors in depth
- Learn about the Gauss-Jordan elimination algorithm and its applications
- Explore the concept of matrix powers and their significance in linear transformations
- Investigate the implications of diagonalization in various mathematical contexts
USEFUL FOR
Students and professionals in mathematics, particularly those studying linear algebra, as well as educators teaching matrix theory and its applications.