Diagrammatic Tensor Notation from the Beginning

[LukeD]

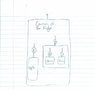
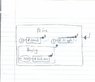
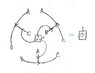
I really liked Penrose's diagrammatic way of writing Tensor algebra, so I spent a while learning the basic notation. Unfortunately, it took a very long time for me to learn this because there is so little info on it to begin with. I also didn't see much mention of how to use the notation for doing numerical computations.

So since I want to be able to use the notation for everything that I should be able to do with tensors, I figured that I'd start at the very beginning of algebra and use the notation. My plan is to write a little tutorial that teaches everything from how to write numbers, vectors & covectors to how to take integrals.

The notation for adding tensors is mine as far as I know, and I've changed some other notation here and there.

I have 14 pages done, but they are very rough. So far they are very basic ideas. Should I continue with this? Any suggestions for cleaning it up? I want to make it as short & simple as possible while still getting the point across.

 

[LukeD]

Pages 4-6

 

[LukeD]

Pages 7-9

 

[LukeD]

Pages 10-12

 

[LukeD]

Pages 13 & 14

I'm thinking of talking about bases next & then tensor products.

 

[LukeD]

Lots of views but not one comment? That makes me sad.

Eventually, I want to get to a point where all of the pictures of the sort on
http://en.wikipedia.org/wiki/Penrose_graphical_notation
make sense.

 

[Ben Niehoff]

It looks pretty good. I've always imagined these objects fitting together sort of like toys. I wouldn't try to actually use the diagrammatic notation to do any real calculations, though...but as a teaching tool, it might be nice. Like teaching linear algebra to elementary school kids...

 

[LukeD]

6 More pages. I decided to do tensor products and contraction before talking about basis vectors and doing numerical calculations.

 

[LukeD]

pages 18-20

 

[LukeD]

12 More.
I got down everything that I wanted for basis vectors, tensor components, and computations.

Here's 21-23

 

[LukeD]

Pages 24-26

 

[LukeD]

Pages 27-28

We dissect the identity

 

[LukeD]

Pages 30-32

These are probably the last ones I'll do for a while. The next topic that I want to do is differentiation, but my Differential Geometry is very weak and I want to be more comfortable with it before I go making up notation for it.

Penrose and Cvitanović both have their own notations for derivatives, but I can't figure out Cvitanović's.

 

[ice109]

i certainly appreciate it thoroughly - i looked for a long time for any info on this stuff and couldn't find anything. the closest thing i could was this book:

http://press.princeton.edu/titles/8839.html

which apparently does stuff with the notation.

have you been in contact with penrose?

 

[LukeD]

No, I haven't been in contact with Penrose at all.
Cvitanovic's book looks fun, but I didn't get much out of it. He draws lots of fun pictures, but he doesn't explain his ideas thoroughly enough for me to understand much.

 

[Rasalhague]

Excellent! I like the uncluttered style and the everyday examples: shopping lists, special offers, etc. Nice, intuitive one-line definition: "Vectors are objects that can be added together or multiplied by numbers." I'm sure anyone who's struggled to learn what a tensor is from the eponymous Wikipedia entry will find this a welcome relief. Are you going to have appendices giving straighter definitions in more formal language and relating it all to conventional notation? I bought Road to Reality recently, partly out of curiosity about this notation, although I've been diverted down lots of detours, trying to figure out other basic stuff... My favorite captions are "a mighty tensor with labels" and "with a basis & a dual basis you can rule the world (of tensors)".

There were maybe one or two places where an extra word of explanation would help. E.g. on the first page, it says "the way the bubbles are connected with lines" doesn't matter, and illustrates this with a 1 connected by one line to a 2 which is connected by one line to a 3 which is connected by two lines to the 1. But 1 is a special number in multiplication; would it mean the same if there were two lines connecting the 2 and 3, or would that mean 1 times 2 times 3 times 2 times 3?

The other thing that I thought might be a bit confusing is the similarity between the notation of a line connecting boxes for the tensor product (as an alternative to the more obvious notation of just sticking the boxes together), and the notation for contraction, but then I noticed you're version is slightly different from Penrose's in that he doesn't use those connector symbols but shows the difference between vectors and covectors by whether their cables point up or down. So his has the advantage of being related to the conventional index placement, but yours has the greater advantage that it can be read upside down, which suits the spirit of coordinate independence!

> in my Mathemagician's Tool.

Tool Box? Tool Kit?

 

[LukeD]

I'm thrilled that you liked it!

Are you going to have appendices giving straighter definitions in more formal language and relating it all to conventional notation?

I probably won't have straighter definitions in terms of vector spaces and the such. You can get those anywhere. I started writing this for my aunt who is dyslexic in hopes that she'll be able to read this notation easier than the usual way of writing algebra. (I've sent her the first pages. She hasn't had time to read them yet.) I'm not writing it for her anymore, but I want to keep things on the level of someone who's had a high school education and probably isn't interested in knowing exactly how things work. However, I expect that most people who read it will already know how everything works anyway.

I might have a few pages on conventional notation if people are interested in my writing more of these.

There were maybe one or two places where an extra word of explanation would help. E.g. on the first page, it says "the way the bubbles are connected with lines" doesn't matter, and illustrates this with a 1 connected by one line to a 2 which is connected by one line to a 3 which is connected by two lines to the 1. But 1 is a special number in multiplication; would it mean the same if there were two lines connecting the 2 and 3, or would that mean 1 times 2 times 3 times 2 times 3?

That's a good point. If I remake that page, I'll be sure to change it to a better example. That was the first page I made, and I wasn't sure what I was going to do about the tensor product notation yet! You'll notice there's a big error. I say "This property is special of numbers", but as long as there are no markers on the lines, it's true of any tensor.

The other thing that I thought might be a bit confusing is the similarity between the notation of a line connecting boxes for the tensor product (as an alternative to the more obvious notation of just sticking the boxes together), and the notation for contraction, but then I noticed you're version is slightly different from Penrose's in that he doesn't use those connector symbols but shows the difference between vectors and covectors by whether their cables point up or down. So his has the advantage of being related to the conventional index placement, but yours has the greater advantage that it can be read upside down, which suits the spirit of coordinate independence!

In the usual notation, you tensor everything together before you do contractions anyway. So it doesn't make a difference. And in my notation - if it's connected by a line in some way, it gets multiplied.

> in my Mathemagician's Tool.

Tool Box? Tool Kit?

It's like a Leatherman Tool http://www.protoolreviews.com/reviews/hand-tools/wrenches-sockets/leatherman-super-tool-300-multitool/image_thumb
but with Math Magic

And what about "Our Standard Basis"?
Maybe I should have called it "This Standard Basis"

 

[Rasalhague]

The monster tensor that needs to be broken down and destroyed (great drawing, by the way) reminds me of the apology that Kip Thorne makes in one of his online lectures about all the bloodthirsty imagery; he'd just been talking gleefully about "strangling" tensors.

In the usual notation, you tensor everything together before you do contractions anyway. So it doesn't make a difference. And in my notation - if it's connected by a line in some way, it gets multiplied.

Yeah, it's not ambiguous. I just thought it might be easier to take in a diagram at a glance if the only lines connecting them were contractions, and the tensor product was shown only by the other method you use: sticking the boxes directly together.

It's like a Leatherman Tool http://www.protoolreviews.com/reviews/hand-tools/wrenches-sockets/leatherman-super-tool-300-multitool/image_thumb
but with Math Magic

Ah, I see. Your Swiss Army tensor-filleter.

And what about "Our Standard Basis"?
Maybe I should have called it "This Standard Basis"

If the underlying set of your manifold is Rⁿ, then I suppose the identity transformation offers a natural choice of coordinate system, the standard basis. Is this the only case where it makes sense to talk about the standard basis? If you have a manifold over n-dimensional Euclidean space conceived of as an affine space, then there's no natural origin and no natural orientation; each of the inifinite number of possible orthonormal bases has a sort of naturalness about is, as the simplest sort of coordinate system, but no one of them is more natural or standard than another. And similarly I think for the generalisation to Riemannian manifolds, but I'm relatively new to all this, and not any kind of expert...

(It gets a bit confusing because some people use the name Euclidean space for the inner product space made of Rⁿ with the usual rules, whereas others reserve the name Euclidean space for an affine space whose associated vector space is made up of Rⁿ with the usual rules.)

 

[LukeD]

Hm... I'm still learning Differential Geometry, but I'm trying to incorporate the various differentiation operators.

One thing I've done is taken the advice of getting rid of using lines for tensor product. Now lines only indicate contractions or free indices.

One thing that I've noticed is that I can interpret the circle on the end of a vector as being a slot to insert a real valued function on a manifold. If I make that identification, then the identity operator works perfectly as the gradient of a function. Inserting a function into the slot on the identity assigns the correct covector.

 

[MathematicalPhysicist]

I must say that I read only the first page, and I found it quite hilarious.
associating numbers with bubbles... :-)

 

[Tokipin]

I really like these!

UML might give you some ideas.

 

[LukeD]

I'm trying to incorporate the ideas from Differential Geometry into my notation. For real valued functions (exterior differential calculus), my notation seems to work pretty well, I'm able to do all of exterior algebra without any pesky (-1)^a terms appearing in the diagrams for the wedge product or exterior derivative at all. (There's no such thing as a "graded Leibniz rule" in the diagrammatic notation, just the normal Leibniz rule.)

My notation seems a little unwieldy though in the non-commutative geometry case of the differential geometry of Lie algebra valued functions since I have vectors in 2 different spaces to worry about. I'm also not too satisfied with my notation for the Lie bracket... It shows up constantly in non-commutative geometry, so it would be nice to have a good notation for it.

I'm currently writing up some very rough pages to show what I mean. I'll have them up shortly. Hopefully even though they're very rough, someone will be able to understand them and give me some suggestions.

 

[LukeD]

It should be noted that I'm using a circle to represent values of one space and a diamond to represent values of a second space.

 

[LukeD]

I don't know if I like my notation for the Lie bracket. I haven't looked at the Jacobi identity yet though. I'd like to find a notation that makes the anti-symmetry of the Lie bracket and the Jacobi identity easy to express.

 

[LukeD]

Ok, here's the last one for now. Is there anyone who understands this stuff better than I who could suggest some better notation for vector valued objects and for the Lie bracket?

 

[LukeD]

Making the vector type symbol smaller makes the Lie bracket much cleaner, but it looks a lot like a contraction between a vector and covector. That could get confusing but anything I've tried to do to clear up that part just looks too cluttered. :(

 

[LukeD]

I believe that I have just written the Jacobi Identity in the coolest way that will ever be discovered.

Seriously, this picture is so beautiful that it should be engraved somewhere.

This picture is supposed to be a 3D shape by the way, but i can't draw it too well. If i could, I'd have all the As together, all the Bs together, and all the Cs together, and then the addition point up at the very top hovering over the whole shape.