Dielectric Constant Computation

[cjX]

Homework Statement

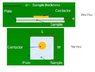
Say, i have a setup as shown on the photo below

http://www.flickr.com/photos/47719498@N07/4375079183/

* setup also seen as attachment

how can i be able to compute for the dielectric constant provided it is not parallel plate and considering two different area is used. one is a circular contact and one is a square-shaped same size as the sample being analyzed.

given are the following:

Capacitance, measured connected with contactors
Area of the contactors, one circular, the other square
Distance - thickness of sample

Homework Equations

Using below Formula:
εr or k is the dielectric constant equivalent to the Capacitance (C ) divided by the Product of ε0, the electric constant and the ratio of Area (A) of the plates t0 their distance (d) between them.

εr = C/(ε0*(A/d))

ε0 = electric constant (8.854E-12)

The Attempt at a Solution

The above formula gives an unreal computed dielectric response to the sample being analyzed

 

[cjX]

can anyone help me pls...

 

[rl.bhat]

To calculate the capacity, you have to take the common area of the contactor and the plate. The dielectric constant of the substance does not depend on the shape of the substance.

 

[cjX]

To calculate the capacity, you have to take the common area of the contactor and the plate. The dielectric constant of the substance does not depend on the shape of the substance.

Sir, meaning to say that only the effective area of both contactor shall be used. if that is the case, the circular contactor area will be used as the reference for computation instead of the plate.

now, capacitance measurement is available but can you pls. help provide direct formula to be used in order to compute for the dielectric constant ? also, fringing lines would happen since the area of the plate is larger than that of the circular contactor. fields would be generated on the area where the circular contactor would not be able to cover.


appreciate your positive response sir.

 

[rl.bhat]

Function of the capacitor is to store the charges. This function is not affected by the fringe lines, because the bound charges on the lower plate are confined in the area equal to the area of the contactor.
Your formula for the dielectric constant is correct.

 

[cjX]

Function of the capacitor is to store the charges. This function is not affected by the fringe lines, because the bound charges on the lower plate are confined in the area equal to the area of the contactor.
Your formula for the dielectric constant is correct.

just to calibrate, i will use the circular contactor for Area on the formula for dielectric constant computation.

now, have told my professor about this and he does not believe that there will be no fringing lines.

can you suggest other formula to be used in calculating the dielectric constant with different area of parallel contactors ? kindly advise for any or reference materials..


thankies

 

[rl.bhat]

now, capacitance measurement is available but can you pls. help provide direct formula to be used in order to compute for the dielectric constant ?
If you can measure the capacitance, then dielectric constant = capacitance with sample/capacitance without sample

 

[Born2bwire]

I doubt anyone can tell you off-hand to what extent the fringing fields will make your system deviate from the ideal parallel plate equation. The equation should give you a good result, perhaps within 10% maybe. I am not aware of anyone doing any true analytical analysis of this kind of problem, maybe if you did a literature search you may find something since this is probably a fairly common situation. That is, I am sure there are texts and papers about the deviations that arise when you have finite parallel plate conductors. Barring that, you could always use a numeric simulation to find your answer, like an FEM or MOM analysis but those are rather involved. In addition, they are more useful for calculating the expected capacitance with a given dielectric configuration. You are doing the opposite, you have the capacitance and wish to find the dielectric from this. So you would probably have to do a variety of results to find out the capacitance as a function of the dielectric and then interpolate from those results what your dielectric constant is.