Dielectric in capacitor: Griffiths question

[person_random_normal]

Hey SIr , (Addressed to Sir J D Grififfiths)

Last year when I took basic electricity and magnetism course , my instructor discussed some interesting ideas which you discussed in your book ''Introduction to Electrodynamics'' ,one of that was calculating force exerted on a dielectric while it's to be inserted in a parallel capacitor(Chapter 4 Electric Fields in matter;page 196-7)
Therein you have made one mistake ! -So said my instructor !
You said -

Reference-

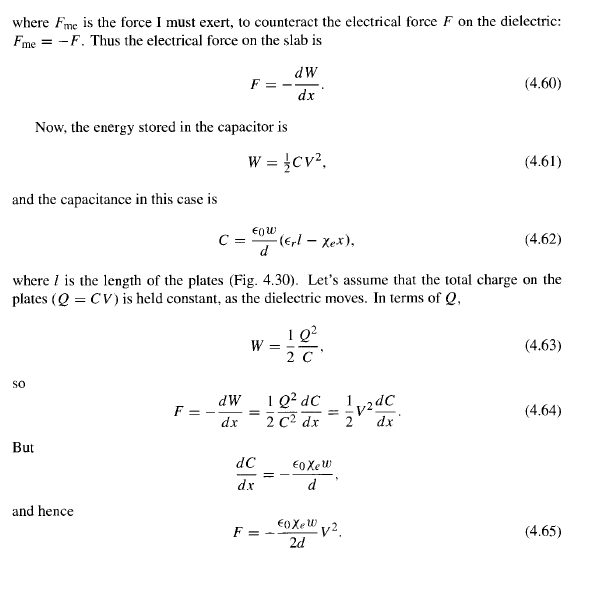
Clarification-
When the capacitor isn't connected to a battery V will change , so the force on dielectric (exerted by capacitor pates) in case when the capacitor plates are maintained at constant potential difference, will differ from the force exerted when the capacitor plates aren't maintained at constant potential difference.

One more thing
When we connect a capacitor to a battery directly , half of the work done by battery is stored in capacitor in form of electrostatic potential energy (and the other half is radiated out in form of electromagnetic radiations)
So,
as of the example of inserting dielectric in parallel plate capacitor , will there be any play of the phenomenon of energy being radiated out in form of electromagnetic radiations (as in the case I mentioned above) ?

Thank you for reading Sir
I am waiting for your reply

Yours enthusiastic student !
-Shreyas Samudra

 

[vanhees71]

I don't see any mistake in the cited derivations in the textbook. It's of coarse the quasistatic approximation, i.e., any radiative effects are neglected.

 

[person_random_normal]

Clarification-
When the capacitor isn't connected to a battery V will change , so the force on dielectric (exerted by capacitor pates) in case when the capacitor plates are maintained at constant potential difference, will differ from the force exerted when the capacitor plates aren't maintained at constant potential difference.

this is what i am talking about - mistake

 

[person_random_normal]

I don't see any mistake in the cited derivations in the textbook. It's of coarse the quasistatic approximation, i.e., any radiative effects are neglected.

See the above reply

 

[vanhees71]

Of course for $Q=\text{const}$ the voltage changes, but that's why Griffiths correctly expresses $W$ in terms of $Q=\text{const}$ rather than $V$ when taking the derivative wrt. $r$.

He also correctly demonstrates what happens when $V=\text{const}$ (e.g., by connected the capacitor to a battery): Then $Q$ changes and one has to take into account both the change of energy due to moving the dielectric against the forces (of the here cleverly neglected fringe fields!) as well as due to the transport of charges through the battery. As I said, I don't see anything wrong in his derivation in both cases.

 

[person_random_normal]

the expression of force on dielectric when Q is constant
1/2 V²dC/dx ....(i)
here V changes as we move the dielectric in or out (-change in capacitance)

the expression of force on dielectric when V is constant
1/2 V²dC/dx ...(ii)
here V stays constant (as we have connected battery)
So , if we take two capacitors with same initial charge and capacitance ,and then insert same kind of dielectric in them following conditions I and II resp.
THEN after having done with insertion , V in case I will not equal V in case II
HENCE force on dielectric in case I will differ from the one in case I

I

 

[vanhees71]

But Griffiths gives a very clear proof in his book. It's as follows

(a) Keep the capacitor charged with total charge $Q$ (disconnected from the battery). The electric energy stored in it is
$$W=\frac{Q^2}{2C},$$
and thus
$$\vec{F}=-\nabla W=\frac{Q^2}{2C^2} \vec{\nabla} C.$$
Now you can get the capacitance with the dielectric moved in by $x$ (as in Griffiths's Fig. 4.30) as a parallel circuit of two parallel capacitances: One capacitor is of length $x$ and width $w$ filled with vacuum (or air) where $\epsilon=1$ and the other part is filled with the dielectric with $\epsilon$ as the dielectric constant. Thus you have (in Heaviside-Lorentz units)
$$C=C_1+C_2=\frac{w}{d}[x+\epsilon_r(l-x)]=\frac{w}{d}(\epsilon_r l-\chi_e x),$$
where $\chi_e=\epsilon_r-1$ is the electric susceptibility of the dielectric. Thus you get
$$\vec{F}=\frac{Q^2}{2C^2} \frac{-\chi_e w}{d} \vec{e}_x=-\frac{V^2 \chi_e w}{2d} \vec{e}_x,$$
which is exactly what Griffth's gets out too.

(b) Capacitor plugged to the battery

Then when moving the dielectric by some infinitesimal $\mathrm{d} x$ the capacitance changes a bit and thus to keep the voltage constant you have to move some charge
$$\mathrm{d} Q=\mathrm{d} x \frac{\mathrm{d}}{\mathrm{d} x}(C V)=\mathrm{d} x V \frac{\mathrm{d} C}{\mathrm{d} x}=-\mathrm{d} x \frac{\chi_e w}{d}.$$
Thus we find
$$F_x=\frac{\mathrm{d}}{\mathrm{d} x} \left (-\frac{C V^2}{2}+V Q \right) = \frac{V^2}{2} \frac{\mathrm{d} C}{\mathrm{d} x} = -\frac{V^2}{2} \frac{\chi_e w}{d},$$
i.e., the same as in case (a). As I said, that's a very clear derivation, and I don't see where there should be a mistake.

Perhaps you can point clearly at the point of the derivation where you think there is one?

 

[person_random_normal]

Oh man I clearly pointed out the mistake
The force in case I is varying not only due to dC/dx but also due to variation in V(potential difference across the plates- it changes as we move the dielectric)
But in case II V will never vary as we have battery, maintaining it constant !

 

[vanhees71]

In case (a) we calculated the change of $V$, which is due to the change in $C$ when expressed in terms of $Q=\text{const}$ and $C$. In case II we have exactly considered the case of constant $V$ which implies that also the charge changes and that you have to take into account the corresponding work done by the battery to provide the change of charge. So we exactly did what you claim we didn't!

 

[person_random_normal]

Look at the final expressions of force
In case one and two
They aren't equal !

 

[vanhees71]

Well, in Griffiths's and my derivation (which are identical) they are the same, and they should obviously be.

 

[person_random_normal]

Look at the final expressions of force
In case one and two
They aren't equal !

Give it a fresh thought
I am sure about it

When we insert dielectric in a parallel plate capacitor(which is not connected to battery)
Q on it will stay constant, but V will change
So, force on dielectric at some instant is
1/2 V^2 dC/dx , wherein V is changing
(x is distance moved by dielectric inside capacitor)

But when the capacitor is connected to battery V is constant,
So force on dielectric at some instant is
1/2 V^2 dC/dx , wherein V is constant

So essentially forces are different in these two cases

 

[vanhees71]

They are not as demonstrated by Griffiths. If you don't want to believe a clear mathematical derivation, I cannot help you.

 

[Jilang]

@shreras, why would you assume that dC/dx is the same in both cases overall the integral?

 

[person_random_normal]

@shreras, why would you assume that dC/dx is the same in both cases overall the integral?

oh

it's just variation of capacitance wrt x (distance moved by dielectric, inside capacitor) - so
of course it's independent of everything else (Q,V ...- whatever)

!

 

[Jilang]

In that case your two expressions in post #21 are identical.

 

[vanhees71]

@shreras, why would you assume that dC/dx is the same in both cases overall the integral?

As the derivation shows, in fact it is. The capacitance doesn't depend on the amount of charge or the applied voltage on the capacitor!

 

[person_random_normal]

In that case your two expressions in post #21 are identical.

of course not

reread it carefully !

 

[Jilang]

I did. The equations are identical instantaneously. Whether V is a constant or not is irrelevant.

 

[Jilang]

As the derivation shows, in fact it is. The capacitance doesn't depend on the amount of charge or the applied voltage on the capacitor!

Quite so. I was just attempting to show why the two expressions must be equal.