Diff eqs with eigenvectors: double roots, but 2nd eigenvector?

[kostoglotov]

The problem is here, I'm trying to solve (b):

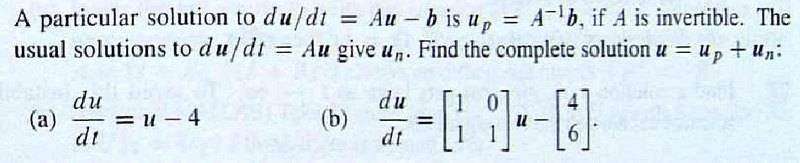
imgur link: http://i.imgur.com/ifVm57o.jpg

and the text solution is here:

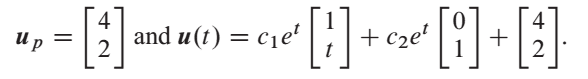
imgur link: http://i.imgur.com/qxPuMpu.pngI understand why there is a term in there with cte^t, it's because the A matrix has double roots for the eigenvalues. What I don't understand is where the (apparent) second eigenvector, <br /> \begin{bmatrix}1\\ t\end{bmatrix} is coming from?

I gave my answer as \vec{u} = \begin{bmatrix}4\\ 2\end{bmatrix} + c_1e^t\begin{bmatrix}0\\ 1\end{bmatrix}+c_2te^t\begin{bmatrix}0\\ 1\end{bmatrix}.

This answer works, but so does the text answer, and it is more complete. But where did that second distinct eigenvector come from?

 

[fresh_42]

It comes from $A_{21} = 1$ and the exponential function but I don't know how to put it correctly. Too long ago.

 

[S.G. Janssens]

This answer works, but so does the text answer, and it is more complete. But where did that second distinct eigenvector come from?

You have a double eigenvalue $\lambda = 1$ with geometric multiplicity one, giving you one eigenvector $v_1 = (0,1)$, and algebraic multiplicity two. So, in order to span the generalised eigenspace corresponding to $\lambda$ (which is just $\mathbb{R}^2$) you need a generalised eigenvector $v_2$, which you can obtain by solving
$$
Av_2 = \lambda v_2 + v_1
$$
(The sequence $\{v_1,v_2\}$ is called a Jordan chain corresponding to $\lambda$ and $v_1$.) Then the solution to the homogeneous system is
$$
u_n(t) = c_1 e^{\lambda t}v_1 + c_2 t e^{\lambda t}v_2
$$
You can see that your own solution is not the most general one, because at time $t = 0$ you cannot satisfy an arbitrary initial condition. (In fact, as you can see you can only satisfy initial conditions $u_0$ for which $u_0 - (4,2)$ is in the span of $(0,1)$.) This is because $v_1$ by itself does not span the generalised eigenspace.

 

[Mark44]

A different approach from the one Krylov took...
Since it is straightforward to get a particular solution to the nonhomogeneous problem, let's look only at the homogeneous system:
$\vec{u}' = A\vec{u}$
This system has a solution $\vec{u} = e^{At}C$, where C is a column matrix of coefficients that depend on initial conditions.

To calculate $e^{At}$, we'll need to calculate the various powers of A.
$A = \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix}$
$A^2 = \begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix}$
$A^3 = \begin{bmatrix} 1 & 0 \\ 3 & 1 \end{bmatrix}$
In general, $A^n = \begin{bmatrix} 1 & 0 \\ n & 1 \end{bmatrix}$
If necessary, this last statement is easy to prove.

$e^{At} = I + At + \frac{A^2t^2}{2!} + \dots + \frac{A^nt^n}{n!} + \dots$
$= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} + t\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} + \frac{t^2}{2!}\begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix} + \dots + \frac{t^n}{n!}\begin{bmatrix} 1 & 0 \\ n & 1 \end{bmatrix} + \dots$
$= \begin{bmatrix} 1 + t + \frac{t^2}{2!} + \dots + \frac{t^n}{n!} + \dots & 0 \\ 0 + t + \frac{2t^2}{2!} + \dots + \frac{nt^n}{n!} + \dots & 1 + t + \frac{t^2}{2!} + \dots + \frac{t^n}{n!} + \dots \end{bmatrix}$
$= \begin{bmatrix} e^t & 0 \\ te^t & e^t \end{bmatrix}$
$= e^t\begin{bmatrix} 1 & 0 \\ t & 1 \end{bmatrix}$
In the matrix a couple of lines up, the expression in the lower left corner is just te^t.

So the solution to the homogeneous problem, $u_h(t)$, is $u_h(t) = e^t\begin{bmatrix} 1 & 0 \\ t & 1 \end{bmatrix}C$,
or, $u_h(t) = c_1e^t\begin{bmatrix} 1 \\ t \end{bmatrix} + c_2e^t\begin{bmatrix} 0 \\ 1 \end{bmatrix}$
In this last form, the two linearly independent eigenvectors are shown.

 

[S.G. Janssens]

Then the solution to the homogeneous system is
$$
u_n(t) = c_1 e^{\lambda t}v_1 + c_2 t e^{\lambda t}v_2 \qquad (*)
$$

Mark44 made me realize that I made a mistake in this line yesterday, my apologies. The method is fine, though. From the Jordan chain you build the correct solution to the homogeneous equation as
$$
u_n(t) = c_1e^{\lambda t}v_1 + c_2e^{\lambda t}(v_2 + t v_1)
$$
I'm sorry for any confusion that I may have caused.

 

[S.G. Janssens]

To make you see the pattern of constructing solutions using Jordan chains more clearly, I will add one example. Suppose you have the homogeneous $3 \times 3$ system corresponding to the matrix
$$
A =
\begin{bmatrix}
1& 0& 0\\
1& 1& 0\\
1& 1& 1
\end{bmatrix}
$$
You can check that $\lambda = 1$ is a triple eigenvalue of geometric multiplicity one. The lone eigenvector is given by $v_1 = (0,0,1)$. To get the first generalised eigenvector, solve
$$
A v_2 = \lambda v_2 + v_1
$$
to obtain $v_2 = (0,1,0)$. Similarly, to get the second generalised eigenvector, solve
$$
A v_3 = \lambda v_3 + v_2
$$
to obtain $v_3 = (1, -1, 0)$. (There is not really a need for Gaussian elimination for these systems: you can find the solutions by inspection.) Then construct the solution as
$$
u_h(t) = c_1 e^{\lambda t} v_1 + c_2 e^{\lambda t}\Bigl(v_2 + \frac{t}{1!}v_1\Bigr) + c_3 e^{\lambda t}\Bigl(v_3 + \frac{t}{1!} v_2 + \frac{t^2}{2!}v_1\Bigr)
$$
where the $c_i$ are constants determined by your initial condition.

In my opinion, taking the matrix exponential directly (as in @Mark44 's post) is faster when it is easy to spot a general formula for the powers of $A$. This is not always the case, in which instance you can rely on computing Jordan chains.

 

[Mark44]

In addition to the technique of calculating $e^{At}$ using powers of A, there's another technique that uses the Cayley-Hamilton theorem, which says that every matrix is a root of its characteristic equation. This technique appears in a Linear Algebra textbook I've hung onto, "Linear Algebra and Differential Equations," by Charles G. Cullen. Cullen's explanation isn't clear to me, so when I figure out what he's doing, I'll post an explanation using that technique.

 

[kostoglotov]

you can find the solutions by inspection.

But by inspection you can see that there are multiple solutions to those equations for the generalized eigenvectors. (0,1,1) would work just as well to solve (A-\lambda I)v_2 = v_1.

 

[Mark44]

So here's the other method I mentioned in my previous post. The technique is presented in "Linear Algebra and Differential Equations," by Charles G. Cullen.

We're solving the DE $\frac{d \vec{u}}{dt} = A \vec{u}$, or $(D - A)\vec{u} = 0$, for which the solution is $\vec{u} = e^{At}C$, where A and C are matrices.
For the problem at hand, $A = \begin{bmatrix} 1 & 0 \\ 1 & 1\end{bmatrix}$

As was already mentioned in this thread, the matrix A has only one eigenvalue: $\lambda = 1$.
The characteristic polynomial for the matrix is $c(x) = (x = 1)^2 = x^2 - 2x + 1$, which is found by evaluating det($\lambda$I - A).

For a diff. equation $(D - 1)^2y = 0$, we would expect a solution of the form $y = c_1 e^t + c_2te^t$.

Per a theorem by Ziebur, cited on page 307 of this textbook, "Every entry of $e^{At}$ is a solution of the nth-order equation c(D)y = 0, where c(x) = det(xI - A) is the characteristic polynomial of A."

That is, $e^{At} = E_1e^t + E_2te^t$, where $E_1$ and $E_2$ are matrices of constants.

At t = 0, the equation above results in $I = E_1$
Differentiating the equation above results in $Ae^{At} = E_1e^t + E_2e^t + E_2te^t$
At t = 0, we have $A = E_1 + E2$

Substituting I for $E_1$ and solving the second equation, we have $E_2 = A - I = \begin{bmatrix} 0 & 0 \\ 1 & 0\end{bmatrix}$

Therefore, $e^{At} = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}e^t + \begin{bmatrix} 0 & 0 \\ 1 & 0\end{bmatrix}te^t$
$= \begin{bmatrix} 1 & 0 \\ t & 1\end{bmatrix}e^t = e^{At}$
Note that the columns of this last matrix hold the two linearly independent eigenvectors.

 

[S.G. Janssens]

But by inspection you can see that there are multiple solutions to those equations for the generalized eigenvectors $(0,1,1)$ would work just as well to solve $(A-\lambda I)v_2 = v_1$.

True, you could equally well work with that choice for $v_2$, but for the same initial condition $u_0$ as before the arbitrary coefficients $c_i$ would then be different and you would end up with exactly the same solution $u_h$ satisfying $u_h(0) = u_0$.

(Note that once you make a different choice for $v_2$, your solution for $v_3$ will also change.)