- #1
shayaan_musta
- 209
- 2
Hi to all experts!
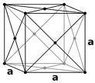
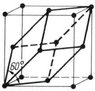
I know individually about primitive cell("It has lattice point at corners only") and unit cell("It has lattice point at corners as well as at center if bcc or at faces if fcc or at bases if it is base centered")
Are these right?
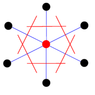
But I don't know what is Wigner-Seitz cell.
But I know that Primitive cell is a special case of unit cell and Wigner Seitz cell is a special case of primitive cell.
Am I right?
Here is space lattice pic. Please identify primitive cell and a unit cell and also a Wigner-Seitz cell in it.
Kindly help me in easiest way.
Thanks for your contribution.
I know individually about primitive cell("It has lattice point at corners only") and unit cell("It has lattice point at corners as well as at center if bcc or at faces if fcc or at bases if it is base centered")
Are these right?
But I don't know what is Wigner-Seitz cell.
But I know that Primitive cell is a special case of unit cell and Wigner Seitz cell is a special case of primitive cell.
Am I right?
Here is space lattice pic. Please identify primitive cell and a unit cell and also a Wigner-Seitz cell in it.
Kindly help me in easiest way.
Thanks for your contribution.