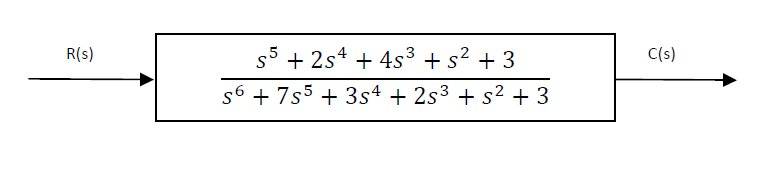SUMMARY
The discussion focuses on deriving a differential equation from a block diagram. The suggested method involves splitting the equation into partial fractions and applying the inverse Laplace transform to each term. This approach is essential for analyzing control systems and signal processing. The conversation highlights the importance of understanding Laplace transforms in the context of block diagram analysis.
PREREQUISITES
- Understanding of block diagram representation in control systems
- Knowledge of Laplace transforms and their properties
- Familiarity with partial fraction decomposition
- Basic concepts of differential equations
NEXT STEPS
- Study the application of Laplace transforms in control theory
- Learn about partial fraction decomposition techniques
- Explore differential equations related to dynamic systems
- Investigate software tools for block diagram analysis, such as MATLAB Simulink
USEFUL FOR
Control system engineers, students studying differential equations, and professionals involved in signal processing and system analysis.