- #1
bob012345
Gold Member
- 2,066
- 896
- TL;DR Summary
- I need some help understanding this block diagram of an analog pendulum circuit. This circuit has a sine generator which complicates the diagram. I need help understanding what comes out of the integrators.
This is an analog circuit block diagram of a mathematical pendulum which solves the equation $$ \ddot{\alpha}= -\frac{g}{l}sin(\alpha)$$.
I need some help following the signals into and out of the blocks. I think the input to integrator #1 must be ##\frac{g}{l}sin(\alpha)## as well as ##\ddot{\alpha}## but what goes into and comes out of integrators #3 and #4? I'm planning on implementing this on The Analog Thing computer. The diagram below comes from Bernd Ulmann's book Analog and Hybrid Computer Programming.
https://the-analog-thing.org/
Thanks for any help!
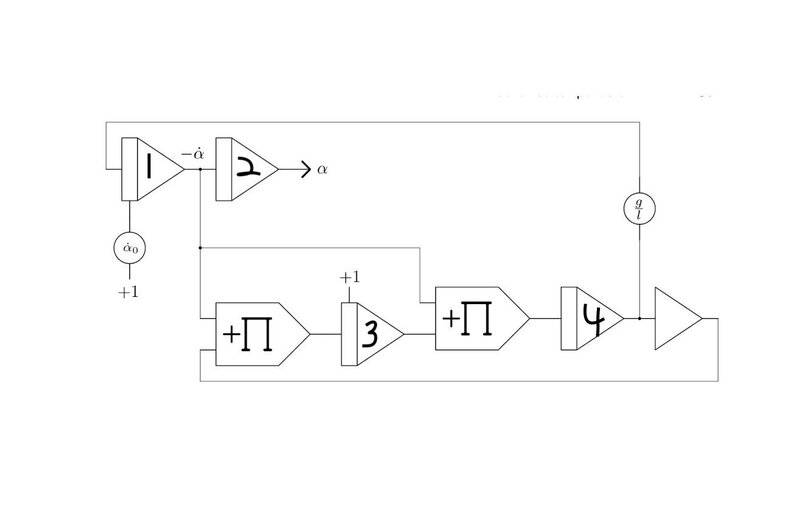
I need some help following the signals into and out of the blocks. I think the input to integrator #1 must be ##\frac{g}{l}sin(\alpha)## as well as ##\ddot{\alpha}## but what goes into and comes out of integrators #3 and #4? I'm planning on implementing this on The Analog Thing computer. The diagram below comes from Bernd Ulmann's book Analog and Hybrid Computer Programming.
https://the-analog-thing.org/
Thanks for any help!