- #1
jrjack
- 111
- 0
Homework Statement
This is a problem from Dynamics but I'm mostly having trouble with the calculus.
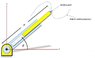
Derive an expression for the position, velocity, and acceleration of a machine in terms of: [itex] r, \dot {r}, θ, \dot{θ}, \ddot{r}, \ddot{θ}, [/itex].
r = length of the arm
θ = angle of the arm to the positive x-axis
[itex] \dot {r}[/itex] = derivative of r with respect to time
[itex] \dot {θ}[/itex] = derivative of θ with respect to time
[itex] \ddot {r}[/itex]= second derivative of r with respect to time
[itex] \ddot {θ}[/itex] = second derivative of θ with respect to timehttps://goo.gl/photos/ZF8Kzn1MEwN69Ev19
Homework Equations
[tex] x=r\cos(\theta); y=r\sin(\theta) [/tex]
[tex] \vec{r} = r\cos (\theta) \hat{i} + r\sin (\theta) \hat{j} [/tex]
I am having trouble combining the product rule and chain rule with multiple variables...
And from there I get lost trying to find the second derivative...
(I last took Calculus 2 about 5 years ago, and have had very little practice since)
The Attempt at a Solution
[tex] \dot{r} = \vec{v} = - \dot{r} \sin (\theta) \dot{\theta} \hat{i} + \dot{r} \cos (\theta) \dot{\theta} \hat{j} [/tex]
Did I apply the chain rule correctly?
or
[tex] \dot{r} = \vec{v} = (-r \sin (\theta) \dot{\theta} + \dot{r} \cos (\theta) \dot{\theta}) \hat{i} + (r \cos (\theta) \dot{\theta} - \dot{r} \sin (\theta) \dot{\theta}) \hat{j} [/tex]
Did I combine the chain and product rules correctly?
Attachments
Last edited: