Physicsdudee
- 14
- 2
- Homework Statement
- Hey,
As you can see in the attachment, I am given a Set that I should integrate a function on. The integrating part should not be a problem, however I am having a hard time figuring out how this set looks like and hence which coordinates to use. I get that the best option would probably be spherical coordinates, but I have to have an idea how this set looks like so I can determine the bounds of integration, that is bounds for φ, Θ and R.
- Relevant Equations
- Spherical coordinates: x=Rsin(Θ)cos(φ), y=Rsin(Θ)sin(φ), z=Rcos(Θ)
Okay so I know, that if the radius is 0, the z coordinate will run from -1 to +1. If the radius tends to one, the z coordinate will tend to 0.
But I still cannot imagine how this set looks like, help would be appreciated.
Thank you.
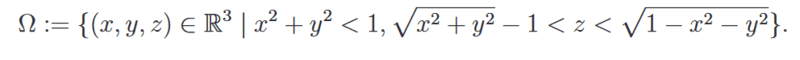
But I still cannot imagine how this set looks like, help would be appreciated.
Thank you.
