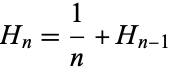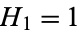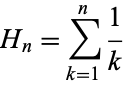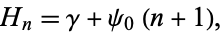Discussion Overview
The discussion revolves around the definitions and properties of the digamma function, denoted as $\psi(n)$, and its relationship with harmonic numbers. Participants explore different formulations and definitions of the digamma function, including potential discrepancies and controversies surrounding these definitions. The conversation includes mathematical reasoning and challenges related to specific values of the digamma function.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants assert that $\psi(n) = -\gamma + \sum_{k=1}^{n-1} \frac{1}{k}$, while others propose an alternative definition $\phi(n) = -\gamma + \sum_{k=0}^{n-1} \frac{1}{k+1}$, highlighting a discrepancy in definitions.
- There is a discussion about the implications of these definitions on the value of $\psi(1)$, with some claiming it leads to different results: $\psi(1) = -\gamma$ versus $\psi(1) = \infty$ depending on the definition used.
- One participant expresses a preference for the factorial function over the gamma function due to confusion regarding its definitions, particularly the relationship between $\Gamma(n)$ and factorials.
- Concerns are raised about the definition of harmonic numbers, specifically regarding the undefined nature of $H_0$ and how this affects the interpretation of the digamma function.
- Some participants reference external sources, such as Wolfram MathWorld, to support their claims about the digamma function and harmonic numbers, but also note contradictions within these sources.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the definitions of the digamma function and its implications. Multiple competing views remain regarding the correct formulation and interpretation of $\psi(n)$ and $\phi(n)$, as well as the handling of specific cases like $\psi(1)$.
Contextual Notes
The discussion highlights limitations in the definitions of the digamma function and harmonic numbers, particularly concerning the treatment of $H_0$ and the implications of different definitions on mathematical outcomes. There is also an acknowledgment of the potential for confusion stemming from the gamma function's definitions.