SUMMARY
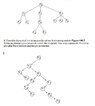
The discussion centers on the concept of drawing a digraph of a binary positional tree. A binary positional tree is defined as a tree structure where subtrees are ordered. The participants clarify that the provided tree illustration does not represent a binary tree. Additionally, there is a request for a definition of how a digraph relates to a positional tree, indicating a gap in understanding this association.
PREREQUISITES
- Understanding of binary trees and their properties
- Familiarity with digraphs and their representations
- Knowledge of tree data structures and positional notation
- Basic graph theory concepts
NEXT STEPS
- Research the properties of binary positional trees
- Learn about digraphs and their applications in data structures
- Study the relationship between trees and graphs in computer science
- Explore visual representation techniques for tree structures
USEFUL FOR
Students, computer science enthusiasts, and software developers interested in data structures, particularly those focusing on tree and graph representations.