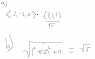SUMMARY
The discussion focuses on calculating the directional derivative at the point (2,0,1) using the gradient and unit vector. The gradient was determined to be <0,-2,0> after finding the partial derivatives. The participants confirmed that the direction of greatest increase is indeed the gradient, and the magnitude of the gradient at this point represents the greatest increase. Additionally, the continuity of the first partial derivatives in the neighborhood of (2,0,1) is essential for the validity of the directional derivative formula.
PREREQUISITES
- Understanding of directional derivatives in multivariable calculus
- Knowledge of gradient vectors and their significance
- Familiarity with partial derivatives and their calculation
- Concept of continuity of functions and derivatives
NEXT STEPS
- Study the properties of gradient vectors in multivariable functions
- Learn about the continuity conditions for partial derivatives
- Explore the application of the directional derivative formula in various contexts
- Investigate the implications of non-continuous partial derivatives on directional derivatives
USEFUL FOR
Students and educators in multivariable calculus, mathematicians focusing on differential calculus, and anyone seeking to deepen their understanding of directional derivatives and gradient vectors.