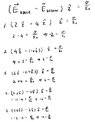OK, let's assume that the electric field above and below the surface is represented by vectors ##~\mathbf E_{\text{above}}## and ##~\mathbf E_{\text{below}}.## We assume no specific direction for either of these fields.
Gauss's law applied to the pillbox shown in the figure says $$\int_S\mathbf E\cdot \mathbf{\hat n}~dA=\frac{q_{\text{encl.}}}{\epsilon_0}$$ where ##\mathbf{\hat n}## is the outward normal. When the height of the pillbox is shrunk to zero, the contributions from the sides vanish and only the contributions from the top and bottom count. This means that $$\mathbf E_{\text{above}}\cdot \mathbf {\hat n}_{\text{above}}dA+\mathbf E_{\text{below}}\cdot \mathbf {\hat n}_{\text{below}}dA=\frac{q_{\text{encl.}}}{\epsilon_0}$$Now the two outward normals point in opposite directions. Let ##~\mathbf {\hat n}_{\text{below}}=-\mathbf {\hat n}_{\text{above}}=-\mathbf {\hat z}.## Then $$(\mathbf E_{\text{above}}-\mathbf E_{\text{below}})\cdot \mathbf {\hat z}=\frac{q_{\text{encl.}}}{\epsilon_0~dA}=\frac{\sigma}{\epsilon_0}.$$ We can simplify this even more by defining scalar components, which could be positive or negative, $$ E_{\text{above}}\cdot \mathbf {\hat z}\equiv E_{\text{above}}^{\perp}~;~~~ E_{\text{below}}\cdot \mathbf {\hat z}\equiv E_{\text{below}}^{\perp}$$in which case we get the boundary condition of the book $$E_{\text{above}}^{\perp}-E_{\text{below}}^{\perp}=\frac{\sigma}{\epsilon_0}.$$Note that, as stated earlier, these z-components can be positive or negative. If one has to show them in a picture, one has to pick a direction. In this case the artist picked them both positive.
The important point to note, and that is why I went through this derivation, is that there is a relative negative sign between the two scalar components regardless of whether they are positive or negative. This means that, if the normal components have opposite signs, the surface charge density has greater magnitude than if they have the same sign. This makes eminent sense in terms of Gauss's law. If electric field lines come out of (or go in from) both the top and the bottom there must be more charge density than if electric field lines come in from the bottom and go out the top, which is what is shown in the picture.