Discontinuous capacitor voltage?

[stroustroup]

Homework Statement

The switches have been in their initial positions for a long time, and switch to the other position at time t = 0s. Find $v_0(t)$ for all t > 0.

Homework Equations

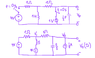
See the attached image for the circuit (I had to draw it because I don't have access to the original image, but I am sure the circuit is the same as the one I was given).

S-domain analysis:
Capacitor of capacitance C is equivalent to uncharged capacitor with impedance 1/sC in parallel with current source with current -Cv(0).

Inductor of inductance L is equivalent to inductor with no initial current and impedance sL in series with a voltage source of -Li(0).

The Attempt at a Solution

The initial conditions are $v_0(0-)$ = 1V and i(0) = 1A (i is current across the inductor)
which you get by replacing C with an open circuit and L with a short circuit (steady-state).

Then the switches go to the other position. I replaced the capacitor and inductor with their equivalent s-domain representations, taking into account their initial conditions, in the second diagram in the image.

Then I used the node voltage method to solve for $V_0(s)$.
$$\frac{v_1-4}{1}+\frac{v_1+1}{s}+\frac{v_1-v_0}{1}=0$$
$$\frac{v_0-v_1}{1} + \frac{v_0}{\frac{2}{s}} - \frac{1}{2}=0$$

$$\left(2+\frac{1}{s}\right)v_1 - v_0 = 4 - \frac{1}{s}$$
$$-v_1 + \left(1+\frac{s}{2}\right)v_0 = \frac{1}{2}$$

By Cramer's rule (or any other method),
$$v_0 = \frac{5-\frac{1}{2s}}{s + \frac{3}{2} + \frac{1}{s}}$$
$$v_0 = \frac{5s-\frac{1}{2}}{s^2 + \frac{3}{2}s + 1}$$

Now I used partial fractions and inverse Laplace transforms to go back to the time domain, which gives me
$$v_0(t) = e^{-\frac{3}{4}t}\left(5\cos\left(\frac{\sqrt 7}{4}t\right)-\frac{17}{\sqrt 7}\sin\left(\frac{\sqrt 7}{4}t\right)\right)$$


Now, the thing that worries me is that, altough I can't find errors in my solution, the voltage of the capacitor at t = 0 clearly isn't continuous. The formula above gives 5V for the initial voltage, but it is 1V before the switch opens. This can also be seen from the Laplace transform by using the initial value theorem.

Is it possible for the capacitor voltage to be discontinous? Or did I mess up somewhere, in the circuit transformations for example?

Actually, what happens if you have a capacitor connected in parallel with two batteries of different voltages, but with a switch allowing to choose either voltage source but not both? Moving the switch should cause a discontinuity in the capacitor's voltage, right?

 

[gneill]

Note that fixed voltage supplies have a Laplace domain representation of V/s, where V is the voltage value. So your 4V supply in your first equation should be 4/s, not just 4.

 

[donpacino]

to answer your question, no it is no possible for the voltage across a cap to be discontinuous, as that would imply infinite current through the capacitor.

real capacitors have resistive and inductive elements to them, as do all wires and real world components. So if you have a cap that is connected to two voltage sources via a switch, you would not be able to determine the cap voltage without knowing the non-ideal elements of the circuit.

does that make sense?

 

[rude man]

Where did the 1V voltage and 1/2 A current sources come from? You can't represent initial conditions that way. Initial conditions disappear eventually whereas your sources are there forever ... at t = infinity those sources are gone!

 

[gneill]

Where did the 1V voltage and 1/2 A current sources come from? You can't represent initial conditions that way. Initial conditions disappear eventually whereas your sources are there forever ... at t = infinity those sources are gone!

True. Although while It would perhaps be more clear if the values of the initial condition "sources" were given some other symbol or if the units were more completely specified, it is fairly common practice to just use the usual source symbols and write current or voltage values for them. It behooves the analyst to treat the values appropriately when it comes to to writing the circuit equations.

The practice is analogous to the way the scaling constant of controlled sources usually omit units required to make units come out right.

For example, an inductor with an initial current can be represented by an inductor in series with a "voltage source" of value $I_o L$. In our case that yields $1H \cdot 1A = 1\;Vs$ (volt-seconds, which also has the designation Weber). One has the option of specifying Vs, Wb, or even VS (where S is the Laplace variable), or just leave it as 1V and "assume" the S.

 

[rude man]

This sounds very dangerous to me, not to say goofy.

 

[gneill]

This sounds very dangerous to me, not to say goofy.

Perhaps, but nevertheless it is done and it works

 

[rude man]

Perhaps, but nevertheless it is done and it works

I think I see whence it derives but I still don't like it!
Cheers.

 

[stroustroup]

Thank you for the help. I had forgotten about this thread for a while, but after reading it I realize I forgot to divide the voltage by s when moving into the s-domain. The time-domain voltage would be 4V * H(t) (step function) and so the Laplace transform is 4 / s.

The capacitor explanation also makes sense. I guess we can't consider them as ideal in that case.