Discover Gliese 581g - Just 20 Light-Years Away!

[Orion1]

abiogenetic RNA...

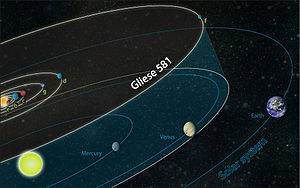
The Gliese 581 star system

The Gliese 581 star system is 7 to 10 billion years old, compared to the Sol star system which is 4.57 billion years old and the age of Earth is 4.54 billion years old.

The oldest ancient fossil microbe-like objects are dated to be 3.5 billion years old.

Gliese 581 g is the fourth known planet in its star system from its parent star.

The planet has an orbital period of just under 37 days, orbiting at a distance of 0.146 AU from its parent star. It is believed to have a mass of 3.1 to 4.3 times that of the Earth and a radius of 1.3 to 2.0 times that of Earth (1.3 to 1.5 times Earth's if predominantly rocky, 1.7 to 2.0 times Earth's if predominantly water ice). Surface gravity is expected to be in the range of 1.1 to 1.7 times Earth's.

If a self-replicating strand of abiogenetic RNA formed there, it would of had 2 to 2.8 times the amount of abiogenetic evolutionary time than that has already occurred on Earth.

Theoretically, there could be highly genetically evolved life forms there, far more evolved than anything that currently exists on Earth, at least with respect to Earth's current bacteria genetic codes.

The most evolved Earth bacteria would genetically be considered 'primitive', compared to Gliese 581 g bacteria.

Gliese 581 g is 20.5 light years away and is also within range for a Panspermia 'courier' to travel the distance in Earth geologic time in 3.5 to 6.5 billion years.

The Panspermia 'courier' velocity differential would be 3.1 to 5.8 lightyears per billion years.
[/Color]
Reference:
http://en.wikipedia.org/wiki/Gliese_581"
http://en.wikipedia.org/wiki/Gliese_581_g"
http://en.wikipedia.org/wiki/Sun"
http://en.wikipedia.org/wiki/Earth"
http://en.wikipedia.org/wiki/Abiogenesis"
http://en.wikipedia.org/wiki/Panspermia"

 

[DaveC426913]

Just because an environment is condusive to carbon based life (which can't possibly be the only type of life out there in such a massive universe) doesn't mean that
... 2. It is more intelligent than simple bacteria or even something as complex as a rabbit

I'd be ecstatic with something as complex as a rabbit.

Sounds like you think the only worthwhile thing is intelligent life...

3. It hasn't become so advanced it has effectively wiped itself out

No one's even talking about intelligent life, but even the ruins of a civilization would be a treasure untold value.

I can't imagine any significant life existing on this planet. If the planet has any sort of atmosphere, then temperature fluctuations would vary wildly with the wind.

Actually, the fact that it is tidally-locked suggests it might have environment that are more stable than Earth. 581g has zones that are temperate all year. No winters to freeze out.

 

[Orion1]

No one's even talking about intelligent life, but even the ruins of a civilization would be a treasure of untold value.

What about bacterial genetic codes that are 2 to 3 times more advanced than anything found on Earth?

Would that also be a treasure of untold value?

Actually, the fact that it is tidally-locked suggests it might have environment that are more stable than Earth. 581g has zones that are temperate all year. No winters to freeze out.

In other words, a perfectly ideal incubator for bacterial evolution, or other higher evolved lifeforms.
[/Color]

 

[ViewsofMars]

The National Science Foundation has a webcast with Steven Vogt and Paul Butler, leaders of a team that discovered the first potentially habitable exoplanet.
http://www.nsf.gov/news/news_videos.jsp?cntn_id=117765&media_id=68454&org=NSF

Also from The National Science Foundation on September 29,
2010:

A team of planet hunters led by astronomers at the University of California, Santa Cruz (UC Santa Cruz), and the Carnegie Institution of Washington, and supported by the National Science Foundation (NSF) and NASA, has announced the discovery of an Earth-sized planet (three times the mass of Earth) orbiting a nearby star at a distance that places it squarely in the middle of the star's "habitable zone," where liquid water could exist on the planet's surface. If confirmed, this would be the most Earth-like exoplanet yet discovered and the first strong case for a potentially habitable one.

This is clearly one of the most exciting areas of science these days" said Ed Seidel, assistant director for NSF's Mathematical and Physical Sciences directorate. "If we do discover life outside our planet, it would perhaps be the most significant discovery of all time."

To astronomers, a "potentially habitable" planet is one that could sustain life, not necessarily one that humans would consider a nice place to live. Habitability depends on many factors, but liquid water and an atmosphere are among the most important.
Please read on . . .
http://www.nsf.gov/news/news_summ.jsp?cntn_id=117765&org=NSF&preview=false

A quote from The Lick-Carnegie Exoplanet Survey: A 3.1M Planet in the Habitable Zone of the Nearby M3V Star Gliese 581 by Steven S. Vogt, R. Paul Butler, E. J. Rivera, N. Haghighipour, Gregory W. Henry, and Michael H. Williamson:

Confirmation by other teams through additional high-precision RVs would be most welcome. But if GJ 581g is confirmed by further RV scrutiny, the mere fact that a habitable planet has been detected this soon, around such a nearby star, suggests that could well be on the order of a few tens of percent, and thus that either we have just been incredibly lucky in this early detection, or we are truly on the threshold of a second Age of Discovery.

SSV gratefully acknowledges support from NSF grant AST-0307493. RPB gratefully acknowledges support from NASA OSS Grant NNX07AR40G, the NASA Keck PI program, and from the Carnegie Institution of Washington. NH acknowledges support from the NASA Astrobiology Institute under Cooperative Agreement NNA04CC08A at the Institute for Astronomy, University of Hawaii, and NASA EXOB grant NNX09AN05G. GWH and MHW acknowledge support by NASA, NSF, Tennessee State University, and the State of Tennessee through its Centers of Excellence program. The work herein is based on observations obtained at the W. M. Keck Observatory, which is operated jointly by the University of California and the California Institute of Technology, and we thank the UC-Keck and NASA-Keck Time Assignment Committees for their support. We also acknowledge the contributions of fellow members of our previous California-Carnegie Exoplanet team in helping to obtain some of the earlier RVs presented in this paper.

We also wish to extend our special thanks to those of Hawaiian ancestry on whose sacred mountain of Mauna Kea we are privileged to be guests. Without their generous hospitality, the Keck observations presented herein would not have been possible. Finally, SSV would like to extend a very special thanks to his wife Zarmina Dastagir for her patience, encouragement, and wise counsel. And even though, if confirmed, the habitable planet
presented herein will officially be referred to by the name GJ 581g, it shall always be known to SSV as ”Zarmina’s World”.
http://www.ucolick.org/~vogt/ms_press-1.pdf

Zarmina's World! I like that.

 

[D H]

I'd be ecstatic with something as complex as a rabbit.

I'd be ecstatic with any life at all, let alone a rabbit.

Actually, the fact that it is tidally-locked suggests it might have environment that are more stable than Earth. 581g has zones that are temperate all year. No winters to freeze out.

A very stable environment could, I think, be a very bad thing for life in this case. Water vapor that falls on the dark side in the form of snow would well stay there a long time without a transport mechanism (e.g., weather). Eventually all of the water could migrate to the dark side. End result: No liquid water, no life.There are, in my mind, too many unknowns to be jumping up and down about this planet as of yet. We don't know if it has an atmosphere. If it does, we don't know it's density, clarity, and makeup. We don't know if it has water, period, let alone liquid water. We don't know if the orbit is nearly circular or not. All of these things are worthy of study because this is the best candidate found yet and because the probability of CHON-based life hinges on these unknowns.

 

[DaveC426913]

I'd be ecstatic with any life at all, let alone a rabbit.

Absolutely!

Some people seem to be saying "ah what's the big deal, they might not even have movie theatres..."

A very stable environment could, I think, be a very bad thing for life in this case. Water vapor that falls on the dark side in the form of snow would well stay there a long time without a transport mechanism (e.g., weather). Eventually all of the water could migrate to the dark side. End result: No liquid water, no life.

Possibly. But there's likely a lot of wind.

There are, in my mind, too many unknowns to be jumping up and down about this planet as of yet. We don't know if it has an atmosphere. If it does, we don't know it's density, clarity, and makeup. We don't know if it has water, period, let alone liquid water. We don't know if the orbit is nearly circular or not. All of these things are worthy of study because this is the best candidate found yet and because the probability of CHON-based life hinges on these unknowns.

Well, OK, it would suck if it didn't have water and an atmo - it'd be just another dead rock.

'course that would just mean we wouldn't know about any subsurface water unless and until we landed on it. Which wouldn't be anytime this century.

 

[Orion1]

A planet with mass of 3.1 to 4.3 times that of the Earth and no atmosphere?

Now that is some good science fiction!
[/Color]

 

[DaveC426913]

A planet with mass of 3.1 to 4.3 times that of the Earth and no atmosphere?

Now that is some good science fiction!
[/Color]

As mentioned, it's also larger in diameter, so surface gravity is closer to 2x Earth.

Who claimed it has no atmo?

 

[Orion1]

.
.
.
.
.

 

[DaveC426913]

.
.
.
.
.

OK, then I guess I don't get what your original "sceince fiction" point was, beyond: yes, if it has no atmo it won't be all that interesting.

 

[Orion1]

.
.
.
.
.

 

[D H]

However, much of the material is the result of supernova residue, so I would expect that such a star system would have planets even more matter rich than Sol's system.

What makes you think that? Your own data contradicts this:

In fact, when I compare the metallicity of the two, this is in fact the case:
Sol metallicity: Z = 0.0177
Gliese 581 metallicity: [M/H] = −0.33 ± 0.12

That negative metallicity means that Gliese 581 has about a half as much metal by concentration than does the Sun.

For example, I would expect Gliese 581 g to have an atmosphere with at least twice the amount of gaseous matter and at least twice as dense

What makes you think that? This is pure speculation. The correlation between body size and atmosphere mass in our solar system is rather low. Venus is only slightly smaller than the Earth but its atmospheric mass is 93 times that of the Earth. Mars' mass is 1/10 that of the Earth but its atmospheric mass is 1/200 that of the Earth. Titan is even smaller than Mars but its atmospheric mass is 20% more than that of the Earth.

and a magnetic field to be at least equivalent to or greater than that of Earth, including the rate at which its core would have cooled despite its age.

What makes you think that? If anything, I would expect just the opposite. Metallicity of the central star is half that of the Sun, and the planet's rotation rate is 1/37 that of the Earth's rotation rate.

Until we learn more about this system, the only thing we can legitimately say about this planet's atmosphere and magnetic field is we don't know.

 

[DaveC426913]

it most certainly had an ocean as well in its geologic history, probably at least twice the volume as Earth's ocean.

I can see you suggesting why it might not be implausible that it has an ocean - but how can you possibly guess about its volume while keeping a straight face?

The Uranian system has a unique configuration among the planets because its axis of rotation is tilted sideways nearly into the plane of its revolution about the Sun, resembling a planet that is tidally locked, yet it has a complex, layered cloud structure, with water thought to make up the lowest clouds, and methane thought to make up the uppermost layer of clouds, therefore I would expect that hot solar driven winds to sweep from the hot side of the planet to the cooler side, and the cooler sided winds to sweep to the hot side of a tidally locked planet as opposed to just everything that is capable of freezing out to simply freeze completely out and condense on only one side.

If single sided freezing were the absolute case than the water vapor that composes the lower cloud bands on Uranus would have been swept to the cooler side, to simply freeze out into crystals and condense onto the surface of the cold side and remain trapped there, yet this is not the case.
[/Color]

Not sure why you're using a gas giant as a comparison to a rocky body. There is not enough surface for gas to condense on. It has to have a complex cloud structure because it's almost entirely atmo.

 

[Brett13]

Am I the only one that HAS heard of this planet before it was talked about on the 29th? I forget what show but it was naked science or how the universe works or something like that. One of them (I forget which) has talked about a rocky planet bigger than the Earth and closer to its star that's in the goldilocks zone around the star gliese 581.. Maybe its just another one in the goldilocks zone?

 

[DaveC426913]

Am I the only one that HAS heard of this planet before it was talked about on the 29th? I forget what show but it was naked science or how the universe works or something like that. One of them (I forget which) has talked about a rocky planet bigger than the Earth and closer to its star that's in the goldilocks zone around the star gliese 581.. Maybe its just another one in the goldilocks zone?

Yes, 581c was the big hopeful several years ago.

It's what inspired me to write my http://www.davesbrain.ca/science/gliese/index.html" .

 

[Vanadium 50]

Before we get too excited, red dwarfs have some problems. One is that many of them - perhaps half - are UV Ceti variables, also called flare stars. They have sporadic flares which are much more dangerous than solar flares - both because they are more energetic (especially in X-rays) and because their planets are closer.

Unfortunately, Gl 581 falls into this category. (When looking it up, it's also NSV 7023. NSV stands for New Suspected Variable)

 

[kamenjar]

...
It's what inspired me to write my http://www.davesbrain.ca/science/gliese/index.html" .

though, I am wondering how would we be able to even in theory do acceleration of 1g for 10 years. in fact that would need to increase over time as the ship's clock decelerates or it's mass increases (I think the effect is the same just explained differently).

I mean, 6 years trip sounds pretty optimistic. I wonder if there's any propulsion tech that is close to getting this achieved.

 

[DaveC426913]

though, I am wondering how would we be able to even in theory do acceleration of 1g for 10 years.

Well, no.

Current proposals for interstellar travel inlcude the Bussard ramjet and Project Orion (which is in principle constructable with existing technology). But they do not reach those kinds of acceleration.

in fact that would need to increase over time as the ship's clock decelerates or it's mass increases (I think the effect is the same just explained differently).

This is not how relativistic travel works.

Its mass increases to an outside observer, and its time dilates to an outside observer, this simply means that the ship will be observed to approach c closer and closer but never reach it.

However, the occupants will not experience any increase in mass, nor any slowing of their clock. And most importantly, they will experience the trip taking only 6 years.

 

[kamenjar]

...

I think I realized what you are saying about mass. That prompted me to post on the Relativity forum. Maybe you can help...

 

[Gaius Baltar]

Just look how misleading this is:

An astronomer picked up a mysterious pulse of light coming from the direction of the newly discovered Earth-like planet almost two years ago, it has emerged.

Read more: http://www.dailymail.co.uk/sciencet...ction-newEarth-planet-year.html#ixzz11eggOi2T

http://www.jb.man.ac.uk/~drl/publications/clf+00.pdf"

http://en.wikipedia.org/wiki/47_Tucanae"

Just goes to show, research goes a long way...

 

[DaveC426913]

Just look how misleading this is:



http://www.jb.man.ac.uk/~drl/publications/clf+00.pdf"

What a terrible article.

Apparently, hey have already decided its composition is "...rocky with liquid water and atmosphere..."

And I like this comment: "It takes just 37 days to orbit its sun which means its seasons last for just a few days."

The one-face Gliese planets do not have seasons.

Nevermind the fact that they give no details about the mysterious light.

 

[Gaius Baltar]

Completely Agree Dave.

It just goes to show, the Media and other sources of news outlets will stop at nothing to promote lies & fear mongering. Shame 60% of people who read, believe...

**Sigh...**

 

[stevebd1]

I mean, 6 years trip sounds pretty optimistic. I wonder if there's any propulsion tech that is close to getting this achieved.

While it's not hard science, I thought this was a great website for ideas and suggestions regarding long distance space travel-

http://www.projectrho.com/rocket/rocket3aj.html

 

[GlieseWorm]

Amazing discovery. Carl Sagan would be thrilled to read this article. Gliese 581g is only 20 light-years away. It would make a nice weekend getaway spot.

http://www.space.com/scienceastronomy/earth-like-exoplanet-possibly-habitable-100929.html

what planet do you live on where 40yrs equates to a weekend? Christ , this is a physics site not Miils n Boom.

 

[GlieseWorm]

could someone offer a physics answer as to when the Gliese 581g existence are due to be officially confirmed or contra-confirmed?

 

[JaredJames]

what planet do you live on where 40yrs equates to a weekend? Christ , this is a physics site not Miils n Boom.

It was a bit of light hearted humour. No need to be so harsh, perhaps a bit less attitude.

could someone offer a physics answer as to when the Gliese 581g existence are due to be officially confirmed or contra-confirmed?

Not entirely sure what else you're looking for here, the above discussion covers things nicely.

 

[lpetrich]

could someone offer a physics answer as to when the Gliese 581g existence are due to be officially confirmed or contra-confirmed?

When someone observes Gliese 581 with a spectroscope with a resolution better than 1 m/s, to translate the Doppler shift into velocity for visible light. Currently, the purported detection of 581g is borderline; improving the spectroscope resolution will make it less borderline.

About spectroscopes better than 1 m/s, I don't know if any are in the works.

There's also the question of how far one can go. Is 1 m/s the limit, or some smaller velocity value?

 

[GlieseWorm]

When someone observes Gliese 581 with a spectroscope with a resolution better than 1 m/s, to translate the Doppler shift into velocity for visible light. Currently, the purported detection of 581g is borderline; improving the spectroscope resolution will make it less borderline.

About spectroscopes better than 1 m/s, I don't know if any are in the works.

There's also the question of how far one can go. Is 1 m/s the limit, or some smaller velocity value?

i have only read of one blip being recorded and the next time they looked the blip didnt appear. to me , if me reading so far is correct, then this would seem to suggest that the confirmation is lacking and that the so called planet is an artefact. combined with the other data that suggests 4 planets not 6, it seems a bit early to come to conclusions about the planet being tidally locked.

if the 'planet' only has a year of 37days, then we should have been seeing a lot more blips by now, and i am not sure we need to request a new spectroscope when what we need is apparently a calendar ?

 

[GlieseWorm]

Some issues on tidal locking:
quoting Wikipedia from yesterday, my additions in bold:
"An estimate of the time for a body to become tidally locked can be obtained using the following formula:[4]

t,lock=wa^6IQ/3Gm^2,pk,2R^5

where
w is the initial spin rate (radians per second)
a is the semi-major axis of the motion of the satellite around the planet
I is the moment of inertia of the satellite (Gliese 581g of course).
Q is the dissipation function of the satellite.
G is the gravitational constant
(m,p) is the mass of the 'planet' (Gliese 581 itself)
(m,s)is the mass of the satellite

k2 is the tidal Love number of the satellite
R is the radius of the satellite.
Q and k2 are generally very poorly known except for the Earth's Moon which has k2 / Q = 0.0011. However, for a really rough estimate one can take Q≈100 (perhaps conservatively, giving overestimated locking times), and

k2=1.5/(1+(19μ/2pgR)

where
p is the density of the satellite
g is the surface gravity of the satellite
μ is rigidity of the satellite. This can be roughly taken as 3×1010 Nm−2 for rocky objects and 4×109 Nm−2 for icy ones.
As can be seen, even knowing the size and density of the satellite leaves many parameters that must be estimated (especially w, Q, and μ), so that any calculated locking times obtained are expected to be inaccurate, to even factors of ten. Further, during the tidal locking phase the orbital radius a may have been significantly different from that observed nowadays due to subsequent tidal acceleration, and the locking time is extremely sensitive to this value."

 

[GlieseWorm]

Some issues on tidal locking:
quoting Wikipedia from yesterday, my additions in bold:
"An estimate of the time for a body to become tidally locked can be obtained using the following formula:[4]

t,lock=wa^6IQ/3Gm^2,pk,2R^5

where
w is the initial spin rate (radians per second)
a is the semi-major axis of the motion of the satellite around the planet
I is the moment of inertia of the satellite (Gliese 581g of course).
Q is the dissipation function of the satellite.
G is the gravitational constant
(m,p) is the mass of the 'planet' (Gliese 581 itself)
(m,s)is the mass of the satellite

k2 is the tidal Love number of the satellite
R is the radius of the satellite.
Q and k2 are generally very poorly known except for the Earth's Moon which has k2 / Q = 0.0011. However, for a really rough estimate one can take Q≈100 (perhaps conservatively, giving overestimated locking times), and

k2=1.5/(1+(19μ/2pgR)

where
p is the density of the satellite
g is the surface gravity of the satellite
μ is rigidity of the satellite. This can be roughly taken as 3×1010 Nm−2 for rocky objects and 4×109 Nm−2 for icy ones.
As can be seen, even knowing the size and density of the satellite leaves many parameters that must be estimated (especially w, Q, and ), so that any calculated locking times obtained are expected to be inaccurate, to even factors of ten. Further, during the tidal locking phase the orbital radius a may have been significantly different from that observed nowadays due to subsequent tidal acceleration, and the locking time is extremely sensitive to this value."

so what i would like to know is for all these claims of tidal locking, what are the estimates or calculated figures used, including errors, plus an experts personal estimates of probability of tidal locking.
any takers?