Telemachus
- 820
- 30
Hi, this thread is an extension of this one: https://www.physicsforums.com/posts/5829265/
As I've realized that the problem is that I don't know how to properly use FFTW, from http://www.fftw.org.
I am trying to calculate a derivative using FFTW. I have ##u(x)=e^{\sin(x)}##, so ##\frac{du(x)}{dx}=\cos(x) e^{\sin(x)}##.
By using the Fourier series I have that: ##u(x)=\displaystyle \sum_{k=- \infty}^{ \infty}\hat u_k e^{ikx}##,
So I must also have: ##\frac{du(x)}{dx}=\displaystyle \sum_{k=- \infty}^{ \infty}ik \hat u_k e^{ikx}##.
I am using that:
##\frac{du(x)}{dx}=\sum_{k=- \infty}^{ \infty} \hat \beta_k e^{ikx}##, with ##\hat \beta_k=ik \hat u_k##.
What I do is, I go to Fourier space, calculate the coefficients of ##u(x)##, multiply by ##ik##, and then I transform back to get the derivative. There are a few things with the FFTW, the first is that the coefficients are unnormalized, so I have to multiply by ##1/N##. I'm not sure if I have to multiply only once, for when I convert from ##u\rightarrow \hat u_k##, or if twice, due to the fact that I am using the coefficients for the derivative ##u\rightarrow \hat u_k\rightarrow \hat \beta_k##.
The other thing has to do with the ordering of the coefficients. In this url: http://www.fftw.org/fftw3_doc/The-1d-Discrete-Fourier-Transform-_0028DFT_0029.html
it says that the coefficients are ordered like:
I am using the discrete versions of the Fourier Transform:
##u_k=\frac{1}{N}\displaystyle \sum_{j=0}^{N-1} u(x_j) e^{-ikx_j}##
##u(x_j)=\displaystyle \sum_{k=-N/2+1}^{N/2} \hat u_k e^{ikx_j}##
However, remember that I'm only going back and forth to Fourier space, so I'm not using this formulas, but I have to have into account the normalization factor, and the correct ordering of the coefficients.
Here is the code:
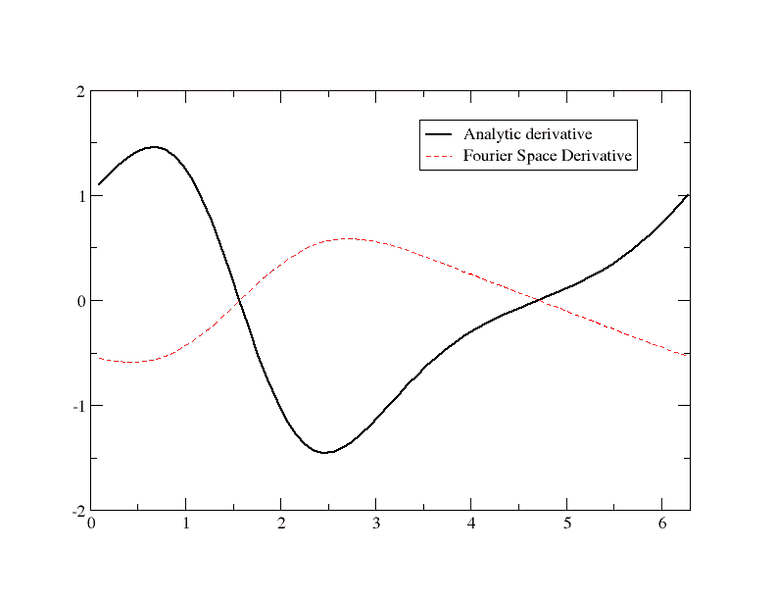
Here is what I obtain:
Thanks in advance.
As I've realized that the problem is that I don't know how to properly use FFTW, from http://www.fftw.org.
I am trying to calculate a derivative using FFTW. I have ##u(x)=e^{\sin(x)}##, so ##\frac{du(x)}{dx}=\cos(x) e^{\sin(x)}##.
By using the Fourier series I have that: ##u(x)=\displaystyle \sum_{k=- \infty}^{ \infty}\hat u_k e^{ikx}##,
So I must also have: ##\frac{du(x)}{dx}=\displaystyle \sum_{k=- \infty}^{ \infty}ik \hat u_k e^{ikx}##.
I am using that:
##\frac{du(x)}{dx}=\sum_{k=- \infty}^{ \infty} \hat \beta_k e^{ikx}##, with ##\hat \beta_k=ik \hat u_k##.
What I do is, I go to Fourier space, calculate the coefficients of ##u(x)##, multiply by ##ik##, and then I transform back to get the derivative. There are a few things with the FFTW, the first is that the coefficients are unnormalized, so I have to multiply by ##1/N##. I'm not sure if I have to multiply only once, for when I convert from ##u\rightarrow \hat u_k##, or if twice, due to the fact that I am using the coefficients for the derivative ##u\rightarrow \hat u_k\rightarrow \hat \beta_k##.
The other thing has to do with the ordering of the coefficients. In this url: http://www.fftw.org/fftw3_doc/The-1d-Discrete-Fourier-Transform-_0028DFT_0029.html
it says that the coefficients are ordered like:
Note also that we use the standard “in-order” output ordering—the k-th output corresponds to the frequency k/n (or k/T, where T is your total sampling period). For those who like to think in terms of positive and negative frequencies, this means that the positive frequencies are stored in the first half of the output and the negative frequencies are stored in backwards order in the second half of the output. (The frequency -k/n is the same as the frequency (n-k)/n.)
I am using the discrete versions of the Fourier Transform:
##u_k=\frac{1}{N}\displaystyle \sum_{j=0}^{N-1} u(x_j) e^{-ikx_j}##
##u(x_j)=\displaystyle \sum_{k=-N/2+1}^{N/2} \hat u_k e^{ikx_j}##
However, remember that I'm only going back and forth to Fourier space, so I'm not using this formulas, but I have to have into account the normalization factor, and the correct ordering of the coefficients.
Here is the code:
Fortran:
program fourser
c...FFTW transformation
double complex zin, zout,duk
parameter (nmax=2**10)
dimension zin(nmax), zout(nmax),duk(nmax)
integer*8 plan1,plan2
double complex zero,zone,eye,kv
real*8 rzero,one
real*8 rmin,rmax,dx
integer N,kn
real*8 x,ct,kr,user,du
data rzero,one,two/0.0d0,1.0d0,2.0d0/
include "/usr/local/include/fftw3.f"
zero = dcmplx(rzero,rzero)
eye = dcmplx(rzero,one)
zone = dcmplx(one,rzero)
Pi = two*dasin(one)
rmin = rzero
rmax = two*Pi
N = 64
dx = (rmax-rmin)/N
c... output files
open(unit=17,file='duan.dat',status='unknown')
open(unit=18,file='duser.dat',status='unknown')
c open(unit=25,file='Invfk.dat',status='unknown')
do i=1,N
x = i*dx
zin(i) = dexp(dsin(x))
c zin(i) = 10.d0*dsin(dabs(x-Pi))**3 - 6.d0*dsin(dabs(x-Pi))
rz = dreal(zin(i))
ri = dimag(zin(i))
ra = cdabs(zin(i))
du = dcos(x)*dexp(dsin(x))
write(17,*) x,' ',du
enddo
c... Direct Fast Fourier Transform
call dfftw_plan_dft_1d(plan1,N,zin,zout,
+ FFTW_FORWARD,FFTW_ESTIMATE)
call dfftw_execute(plan1)
c... Solution coefficients
do i=1,N
duk(i) = eye*(i)*zout(i)/N
enddo
c... Inverse Fast Fourier Transform
call dfftw_plan_dft_1d(plan2,N,duk,zout,
+ FFTW_BACKWARD,FFTW_ESTIMATE)
call dfftw_execute(plan2)
call dfftw_destroy_plan(plan1)
c... Solve derivative
do j=1,N
x = j*dx
user = dreal(zout(j))/N
cuser = dimag(zout(j))
write(18,*) x,' ',user
enddo
close(17)
close(18)
call dfftw_destroy_plan(plan2)
stop
endHere is what I obtain:
Thanks in advance.