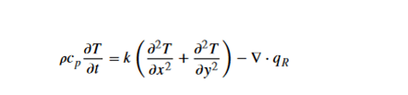Displaying the dimensionless Radiation Transport Equation

In summary, the conversation discusses the display of the Radiation Transport Equation (RTE) in a dimensionless form. The picture of the RTE is shown and the speaker would like to include the Planck number (N), as well as the Prandtl number and Rayleigh number. They have attempted to do so, but have not been successful and are seeking help in understanding the process. Boby asks about the scaling of variables and how time is scaled, as well as how \mathbf{q}_R is defined in terms of temperature and its derivatives.
  • #1
BigBoBy17
1
0
TL;DR Summary
Display the Radiation Transport Equation dimensionless
Hallo,
I would like to display the RTE (Radiation Transport Equation) dimensionless. In the picture, the RTE is shown. I would like to have the Planck number (or N) inside at the end. Additionally, the Prandtl number and the Rayleigh number can be inside. I have already many attempts behind me, but I do not get it. Could someone help me and explain it to me? I would be very grateful.
RTE.png

Boby
 

Attachments

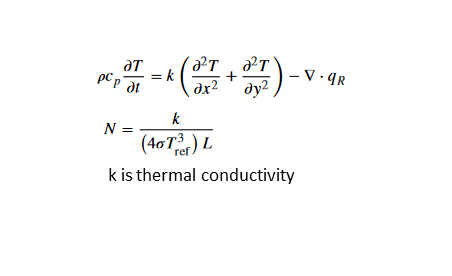
  • RTE.png
    RTE.png
    3.2 KB · Views: 88
Physics news on Phys.org
  • #2
How are you scaling the variables? I assume temperature scales with [itex]T_{\mathrm{ref}}[/itex] and lengths with [itex]L[/itex]; that leaves the question of how you scale time. As you mention Rayleigh and Prandtl numbers, this scaling presumably comes from the momentum equation, which you haven't included in your post.

How do you define [itex]\mathbf{q}_R[/itex] in terms of [itex]T[/itex] and its derivatives?
 

FAQ: Displaying the dimensionless Radiation Transport Equation

What is the dimensionless Radiation Transport Equation?

The dimensionless Radiation Transport Equation is a mathematical equation used to describe the transport of radiation through a medium. It takes into account the absorption, scattering, and emission of radiation within the medium.

Why is it important to display the dimensionless Radiation Transport Equation?

Displaying the dimensionless Radiation Transport Equation allows us to understand the behavior of radiation in different materials and environments. It also helps us to make predictions and calculations for various applications, such as in nuclear reactors or medical imaging.

How is the dimensionless Radiation Transport Equation derived?

The dimensionless Radiation Transport Equation is derived from the Boltzmann Transport Equation, which is a more general equation used to describe the transport of particles through a medium. By simplifying the Boltzmann equation and making certain assumptions, we can arrive at the dimensionless form of the equation.

What are the variables in the dimensionless Radiation Transport Equation?

The dimensionless Radiation Transport Equation has several variables, including the radiation intensity, the absorption and scattering coefficients of the medium, and the source term. These variables can be further broken down into parameters such as energy, direction, and position.

How is the dimensionless Radiation Transport Equation used in practical applications?

The dimensionless Radiation Transport Equation is used in a variety of practical applications, such as in nuclear reactor design, radiation shielding, and medical imaging. It allows us to predict and control the behavior of radiation in these scenarios, ensuring safety and efficiency in various industries.

Similar threads

A Equipartition of energy in the modes of a resonant cavity
Replies
4
Views
1K
B Physical temperature and antenna temperature
Replies
3
Views
834
I Demo for Moments of RTE (Radiative transfer equation)
Replies
1
Views
917
I What happens if you increase μ0 and decrease ϵ0? Or vice versa
2
Replies
68
Views
4K
"Holographic" Display with Rotating Blades
Replies
15
Views
4K
Bernoulli vs. Reynold Transport Theorem Problem for Raincap
Replies
11
Views
2K
I Understanding Parallel Transport
Replies
9
Views
6K
Elevated Geiger Counter Radiation Reading for Envelope?
Replies
26
Views
2K
I Electromagnetic radiation, photons, quantized energy levels
Replies
1
Views
920
Is hv/kt Dimensionless in Planck's Radiation Law?
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top