Distance to the nearest node along the back wall

[lodestar]

Homework Statement

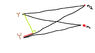
Two 512Hz tuning forks are placed 3.0 m apart on the bench at the front of a classroom. Each is 2.0 m from a side wall and the room is 7.0 m. The speed of sound is 343 m/s.
b) If the back wall room is 10.0 m away what is the distance from the back corner of the room to the nearest node along the back wall?

Homework Equations

wavelength = speed/frequency
Path length difference = (n-1/2)λ

The Attempt at a Solution

The wavelength of sound is found to be 0.67m (wavelength = 343 m/s / 512 Hz).
path length difference = x - (3.5 - x) = 2x - 3.5 m
2x - 3.5m = (n-1/2)λ
x = [(n-1/2)λ + 3.5m]/2
node = 1
x = 1.92 m

I have partial answers from my teacher. The central anti node is 3.5 m from the corner. The first node is 1.12 m from the central antinode. The second node is 3.35 m from the central anti node. The third node is 5.58 m (beyond the corner). The second node is 3.5 - 3.5 = 0.15 m from the corner. I do not understand how to find the distances of these nodes from the central anti node.

 

[andrevdh]

This sounds (unintentional pun) like a double slit problem.

 

[haruspex]

It's just geometry. Draw a diagram of the room. Mark an antinode, say, at distance x from the central antinode. How far is it from there to each fork?

 

[andrevdh]

Node would be destructive interference.

 

[Wily Willy]

It does sound like a double slit problem.

lodestar,

I think it would help you to recall two things: why there is a node centered between the two forks and the wave equation.

 

[Wily Willy]

Anti-node is destructive I believe.

 

[haruspex]

Anti-node is destructive I believe.

No, andrevdh is right.

 

[andrevdh]

T₁ and T₂ are the two tuning forks.
The path length difference between the two waves is the distance Δ in the drawing .
Which is (n - 1/2)λ as you mentioned.