Homework Help Overview
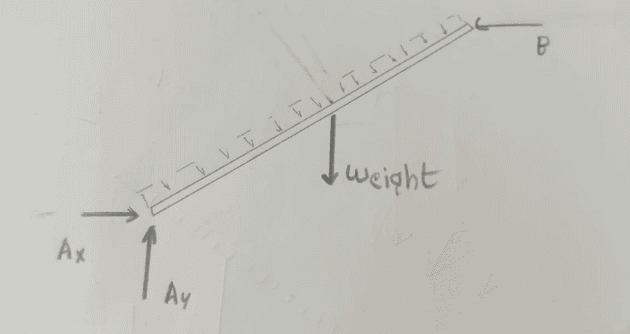
The discussion revolves around the representation of a distributed load on an inclined beam, specifically how to accurately depict this load in a free body diagram. Participants are exploring the nature of the load, its direction, and the implications of the beam's inclination on the load's representation.
Discussion Character
- Conceptual clarification, Problem interpretation, Assumption checking
Approaches and Questions Raised
- Participants question whether the distributed load should be represented as rectangular or triangular and discuss the implications of the beam's angle on the load's direction. There are attempts to clarify the nature of the distributed load, with some suggesting it should be vertical while others express confusion about how to depict it accurately.
Discussion Status
There is active engagement with multiple interpretations of how to represent the distributed load. Some participants have provided insights into the nature of the load, while others are seeking visual aids to better understand the free body diagram. Guidance has been offered regarding the uniformity of the load and its representation.
Contextual Notes
Participants are navigating the complexities of drawing free body diagrams under specific conditions, including the weight per unit length of the beam and the effects of inclination. There is mention of a specific weight value and references to external resources for further clarification.
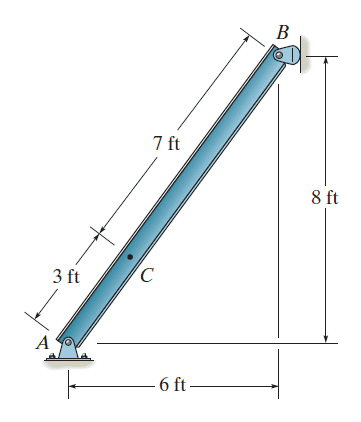 please help me understand how to draw the free body diagram for this one.
please help me understand how to draw the free body diagram for this one.