Distribution of normal force in this problem

[Rikudo]

Homework Statement

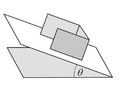
A cardboard strip, folded in U shape, is placed on an inclined plane, as shown in the figure. Length of the two parallel sections is n = 1.5 times of the length of the middle section,that is a square. At what minimun angle of inclination theta will the cardboard topple? Friction is sufficient to prevent sliding

Relevant Equations

Torque

It is crystal clear that we need torque equation to solve this. But, in order to do so, I need to know where the normal force is located. As far as I'm concerned, normal force is not distributed equally. If this is true, then I suppose this problem is unsolvable? (Though the book says thay it is possible to solve them)

 

[malawi_glenn]

When you have a solid homogenous block on an incline, where do you assign the normal force?

 

[Rikudo]

Well, if I assume that the normal force is distributed equally, then the most plausible answer is at the CoM.

But, after I read this site, especially the 2nd paragraph of the answer, I doubt that it is alright to make this assumption.

https://physics.stackexchange.com/questions/356506/distribution-of-normal-force-on-a-book-resting-on-the-edge-of-a-table#:~:text=No, the normal force is,with the conditions for equilibrium.

Here is a part of the statements that I took from it.

"The weight of the book is distributed uniformly because its mass is distributed uniformly, but there is no reason why normal reaction should be distributed uniformly also."

 

[Orodruin]

But, in order to do so, I need to know where the normal force is located.

No, you do not. All you need to know is where it needs to be located to prevent tipping and whether that is admissable or not.

 

[malawi_glenn]

Well, if I assume that the normal force is distributed equally, then the most plausible answer is at the CoM

Inside the block? Isn't the normal force a contact force between two surfaces?

Anyway, the point I wanted to approach was this: when it flips - where will the normal force be?

Have you done this calculation yet, it is a similar problem.
A homogenous ruler is placed at the edge of a table so that a part of the ruler sticks out. How big mass can you put on the side that sticks out so that the ruler does not tip over?

 

[Rikudo]

where will the normal force be?

At the edge of the block, I guess?

 

[Orodruin]

At the edge of the block, I guess?

… and therefore…

 

[Rikudo]

Ahh! So, we only need to take into account the normal force at the section that is perpendicular to the two others!

 

[Orodruin]

The thing is, for there to be torque equilibrium, the net normal force plus friction must act along the same line as the weight. This can only occur if the center of mass is above the region of support. If the com acts along a line outside the region of support, the object will have a net torque and fall over.

 

[Rikudo]

A homogenous ruler is placed at the edge of a table so that a part of the ruler sticks out. How big mass can you put on the side that sticks out so that the ruler does not tip over?

So, when calculating the torque, we only use the weight of the ruler, the weight of the mass, and the normal force at the edge of the table. Am I correct?

 

[Lnewqban]

Could you determine the spatial location of the center of mass of that folded U shape?

 

[haruspex]

Could you determine the spatial location of the center of mass of that folded U shape?

As is often the case, but more particularly with moments of inertia of compound shapes, that's not quite the simplest way.

 

[Lnewqban]

As is often the case, but more particularly with moments of inertia of compound shapes, that's not quite the simplest way.

Would you mind explaining your statement a little more, please?

 

[haruspex]

Would you mind explaining your statement a little more, please?

Just take the balance of moments of the simple shapes about the tipping axis. Each is a function of the angle.
I find it is rarely worth the bother of finding the mass centre of such an assembly, unless that is the specific aim.

 

[Lnewqban]

Ahh! So, we only need to take into account the normal force at the section that is perpendicular to the two others!

@Rikudo, were you able to solve this problem?

 

[Rikudo]

@Rikudo, were you able to solve this problem?

Yes