Question about friction in a problem with a stick and cylinder

[Matt Raj]

Homework Statement

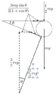
A horizontal stick of mass m has its left end attached to a pivot on a plane inclined at an angle θ, while its right end rests on the top of a cylinder also of mass m which in turn rests on the plane, as shown in Fig. 2.36. The coefficient of friction between the cylinder and both the stick and the plane is μ.
(a) Assuming that the system is at rest, what is the normal force from the plane on the cylinder?

Relevant Equations

T=rxF
Ff=µ*N

The friction from the rod and the friction from the plane on the cylinder should be the same due to torque equilibrium on the cylinder. If we let N_1 be the normal force on the rod and N_2 be the normal force on the cylinder from the plane, I expected µN_1 = µN_2. Looking at torque on the rod, mg/2=N_2. Thus N_1 = mg/2, but this clearly isn't correct. The normal force on from the plane should be greater than N_1 and the correct answer is 3mg/2 which I got from writing the equations only in terms of equal frictions and not using the equation µN_1 = µN_2 and instead using F_1=F_2, where F_1 is the friction from the rod and F_2 is the friction from the plane.

Is the reason my first method was wrong because the given µ in the problem is simply the maximum possible value for friction and in this problem, the frictions are equal but both have different normal forces and µ values less than the given µ?

 

[tnich]

Is the reason my first method was wrong because the given µ in the problem is simply the maximum possible value for friction and in this problem

I think this reasoning is correct. An object resting on a level surface with a coefficient of friction $\mu$ does not experience a horizontal force. The force $\mu mg$ is just maximum force due to friction on an object that is not slipping.

However, I don't understand why you think the normal force is $\frac 3 2 mg$. Since everything is at rest, surely the vertical force of the plane on the cylinder would have to equal the weight of the cylinder plus half the weight of the rod, or $\frac 3 2 mg$. But the vertical force is not equal to the normal force on the cylinder unless $\theta=0$.

 

[TSny]

However, I don't understand why you think the normal force is $\frac 3 2 mg$. Since everything is at rest, surely the vertical force of the plane on the cylinder would have to equal the weight of the cylinder plus half the weight of the rod, or $\frac 3 2 mg$. But the vertical force is not equal to the normal force on the cylinder unless $\theta=0$.

It turns out that the normal force, $N$, that the plane exerts on the cylinder does equal $\frac 3 2 mg$, independent of $\theta$. That surprised me at first. But, a quick way to see that $N = \frac 3 2 mg$ is to consider the net torque on the cylinder with the origin for torques taken at the point on the plane where the rod is pivoted.

 

[tnich]

It turns out that the normal force, $N$, that the plane exerts on the cylinder does equal $\frac 3 2 mg$, independent of $\theta$. That surprised me at first. But, a quick way to see that $N = \frac 3 2 mg$ is to consider the net torque on the cylinder with the origin for torques taken at the point on the plane where the rod is pivoted.

But wouldn't that make the upward force of the plane on the cylinder more than $\frac 3 2 mg$? That would mean the whole system is accelerating upward. My first thought when I saw this problem was that it might be physically unrealizable. Perhaps that is the case.

 

[hutchphd]

But wouldn't that make the upward force of the plane on the cylinder more than 32mg32mg\frac 3 2 mg?

Remember the static friction is less than a maximum. At some angle it will be insufficient.

 

[tnich]

Remember the static friction is less than a maximum. At some angle it will be insufficient.

I don't think it works for any angle except zero. Besides, $\mu$ is not even in the equations when balancing the torques about the rod pivot point. We need to satisfy both the force balance and the torque balance equations, and the torque has to balance regardless of the torque origin. That does not seem to be possible for this problem. Try to balance the torques about the center of the cylinder. Then try again about the point where the rod touches the cylinder. Can you make the three torque balance equations work using the same upward force of the plane on the cylinder?

 

[hutchphd]

Consider when the angle is small but nonzero. For any nonzero μ there will be enough friction to keep the roller from rolling. So solution exists.

 

[TSny]

But wouldn't that make the upward force of the plane on the cylinder more than $\frac 3 2 mg$?

How so? Can you show an equation that reflects your thoughts here?

 

[tnich]

How so? Can you show an equation that reflects your thoughts here?

I was just having difficulty drawing a free body diagram that captured the problem. I think I have it now, and I have convinced myself that the torque balances for three different pivot points.

 

[TSny]

@tnich, your FBD looks good.