Torque on Rod Due to Normal Force at a Hinge

[erfz]

Homework Statement

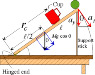
In this diagram,

I wondered if there is any torque due to the normal force from the hinge, once the support stick is removed. I also want to know what the normal force would be at the hinge. The cup and ball are to be ignored here (essentially massless).

Homework Equations

$F_{net} = ma$
$\tau_{net} = I\alpha$
$\tau = Frsin(\phi)$, where $\phi$ is the angle between F and r

The Attempt at a Solution

My assumption would be yes: there is a torque due to the normal force acting straight up from the hinge on the point touching the table. However, the solution to the problem measures torque from the hinge axis (going in and out of the page), and states that the torque is $\tau_{net} = Mgcos(\theta)\frac{L}{2}$.
I'm confused by this, but I feel that there are two possibilities here:

1. The torque due to the hinge is somehow 0
2. The "net" in the expression $\tau_{net} = I\alpha$ depends on the axis it is measured with respect to, just like $\tau = Frsin(\phi)$. That is to say that the only torques that contribute to the net are those not acting at the axis of choice.

Is one of my suppositions correct?

As for the normal force at the hinge, I was thinking that I could say that $F_{net, ~vertical} = Mg - N$ at the center of mass? This happening at only the center of mass is just a guess. So then, if I go through $\tau = I\alpha = \frac{1}{3}ML^2 \alpha = Mgcos(\theta)\frac{L}{2}$, I can derive that $\alpha = \frac{3g}{2L}cos(\theta)$ and that the linear acceleration down from this is $a_{down} = \alpha cos(\theta) \frac{L}{2}$. Using this for the $F_{net}$, I get that $a_{down} = g - N$, so $N = g - a_{down}$.
Is this reasoning correct here?

Thanks!

 

[haruspex]

torque due to the normal force

Torque due to a force is only meaningful in respect of a specified axis. Which axis do you mean?
In particular, if a force acts at a point P then it creates no torque about P.

 

[erfz]

Torque due to a force is only meaningful in respect of a specified axis. Which axis do you mean?
In particular, if a force acts at a point P then it creates no torque about P.

I see. I meant the axis at the hinge, going in and out of the page.
So this means that supposition 2 is the accurate one.

 

[haruspex]

I see. I meant the axis at the hinge, going in and out of the page.
So this means that supposition 2 is the accurate one.

Yes, but they are both true.

 

[erfz]

Torque due to a force is only meaningful in respect of a specified axis. Which axis do you mean?
In particular, if a force acts at a point P then it creates no torque about P.

Yes, but they are both true.

Fantastic!
Is there anything wrong you see with my reasoning of the normal force?

 

[haruspex]

Is there anything wrong you see with my reasoning of the normal force?

There seem to be some other forces with vertical components, from the stick, the ball and the cup.
But you have not actually stated the problem that goes with the diagram, so it is hard to say. You mention accelerations, for example.

 

[erfz]

There seem to be some other forces with vertical components, from the stick, the ball and the cup.
But you have not actually stated the problem that goes with the diagram, so it is hard to say. You mention accelerations, for example.

Sorry I should've made it more clear that I'm only considering the system after the supporting stick is removed and that the ball and cup are massless.
I'm really only considering the rod and the hinge for what I'm asking.

 

[haruspex]

Sorry I should've made it more clear that I'm only considering the system after the supporting stick is removed and that the ball and cup are massless.
I'm really only considering the rod and the hinge for what I'm asking.

Ah, yes, I did see that earlier but when I came back to the thread I forgot. A risk with multitasking.

at the center of mass?

For linear force analysis, the line of action does not matter, only the direction.

The rest of your work looks fine, except that you forgot to divide N by M at the end.

 

[erfz]

For linear force analysis, the line of action does not matter, only the direction.

Sorry, I'm not sure what you mean by this. Do you mean the analysis does not require forces be considered at the center of mass? How can that be if different points on the rod have different linear accelerations downward?

The rest of your work looks fine, except that you forgot to divide N by M at the end.

Haha silly error on my part.

 

[haruspex]

Sorry, I'm not sure what you mean by this. Do you mean the analysis does not require forces be considered at the center of mass? How can that be if different points on the rod have different linear accelerations downward?

If a force F is exerted on a rigid mass m (floating in space, say) then the acceleration of its mass centre is F/m. The force can be exerted at any point and at any angle. Its line of action does not need to pass through the mass centre.

 

[erfz]

If a force F is exerted on a rigid mass m (floating in space, say) then the acceleration of its mass centre is F/m. The force can be exerted at any point and at any angle. Its line of action does not need to pass through the mass centre.

That's great to know, but I'm not sure why you bring it up. Is there something in my work that contradicts this statement? My main assumption was that the force analysis is to be considered at the center of mass, which is important since every point on the bar has different downward acceleration (proportional to the distance from the hinge). That is to say that $M_{cm} a_{cm, ~down} = M_{cm}g - N$.

 

[haruspex]

That's great to know, but I'm not sure why you bring it up. Is there something in my work that contradicts this statement? My main assumption was that the force analysis is to be considered at the center of mass, which is important since every point on the bar has different downward acceleration (proportional to the distance from the hinge). That is to say that $M_{cm} a_{cm, ~down} = M_{cm}g - N$.

Because you wrote:

I was thinking that I could say that $F_{net, ~vertical} = Mg - N$ at the center of mass? This happening at only the center of mass is just a guess.

 

[erfz]

So is that to say that I was correct in my assumption?

 

[haruspex]

So is that to say that I was correct in my assumption?

Yes.

 

[erfz]

Yes.

Wonderful. Thank you for all your help!