Devin-M
- 1,076
- 765
On second thought, I myself cropped @collinsmark ’s TIFs in photoshop during my analysis so maybe I inadvertently corrupted his data.
The discussion centers on the effects of destructive interference in a double slit experiment using starlight, specifically when employing an H-Alpha narrowband filter (656nm +/- 3nm). Participants clarify that in a simple two-slit setup, energy is spatially redistributed rather than reflected back to the source, with reductions in energy at destructive interference points balanced by increases at constructive interference points. The conversation also highlights discrepancies in expected versus observed red values (analog to digital units) when comparing single and double slit configurations, emphasizing that different setups yield different energy distributions.
PREREQUISITESAstronomy enthusiasts, astrophotographers, and physics students interested in the practical applications of interference patterns and energy conservation principles in optical experiments.
I tend to use "noise" to mean anything that is not signal. Here that would mean stray and scattered light, noise from the photodiode junction (dark current) and associated electronics. It is the nature of these systems that the "noise" will average to a nonzero offset. Not all of it is simply characterized nor signal dependent. But it does need to be subtracted for accuracy of any ratio.Drakkith said:What is the definition of 'noise' here? My understanding is that noise is the random variation in the pixels that scales as the square root of the signal.
What do you define as 'noise' here? What are you actually computing when you compute the 'noise'? I suspect you and I may mean something different when we use that word.Devin-M said:Edit: nevermind, it probably doesn’t account for the discrepency because noise from the background sky glow would be expected to double with the double slit, so the math wouldn’t work out.
When the lens cap is on (same exposure settings as the light frame), there is still still ADUs per pixel even through there is no light. With a large enough sample, for example 100x100 pixels, red is 1/4th of the bayer pattern so you have 2500 samples. So you add up the ADUs of all the pixels combined, then divide by the number of pixels. That’s the average noise per pixel. If you look pixel by pixel, the values will be all over the place but when you move the 2500 pixel selection around the image, the average noise is very consistent across the image.Drakkith said:What do you define as 'noise' here? What are you actually computing when you compute the 'noise'?
Devin-M said:@collinsmark The only other uncertainty I have… when you cropped those TIF files, perhaps in photoshop, did they possibly pick up a sRGB or Adobe RGB gamma curve?
I believe simply saving a TIF in photoshop with either an sRGB or Adobe RGB color profile will non-linearize the data by applying a gamma curve. This doesn’t apply to RAW files. (see below)
Okay, you're measuring the combined dark current + bias + background signal, using a large sample of pixels to average out the noise (the randomness in each pixel) to get a consistent value. No wonder I've been so confused with what you've been doing.Devin-M said:When the lens cap is on (same exposure settings as the light frame), there is still still ADUs per pixel even through there is no light. With a large enough sample, for example 100x100 pixels, red is 1/4th of the bayer pattern so you have 2500 samples. So you add up the ADUs of all the pixels combined, then divide by the number of pixels. That’s the average noise per pixel. If you look pixel by pixel, the values will be all over the place but when you move the 2500 pixel selection around the image, the average noise is very consistent across the image.
I turned uploading back on. Could you spare a raw file of the single slit and one of the double slit? My RawDigger app seems to only open RAW files. It won’t even open a TIF or JPG so I resorted to manually entering all the pixel values into a spreadsheet to get the averages.collinsmark said:Btw, @Devin-M, is your program capable of working with .XISF files? I usually work with .XISF files from start to finish (well, until the very end, anyway). If your program can work with those I can upload the .XISF files (32 bit, IEEE 754 floating point format) and that way I/we don't have to worry about file format conversions.
[Edit: Or I can upload FITS format files too. The link won't let me upload anything though, presently.]
Devin-M said:I turned uploading back on. Could you spare a raw file of the single slit and one of the double slit? My RawDigger app seems to only open RAW files. It won’t even open a TIF or JPG so I resorted to manually entering all the pixel values into a spreadsheet to get the averages.
collinsmark said:Here are the resulting plots:
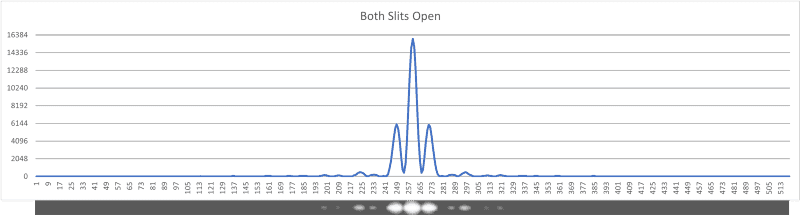
Figure 8: Both slits open plot.
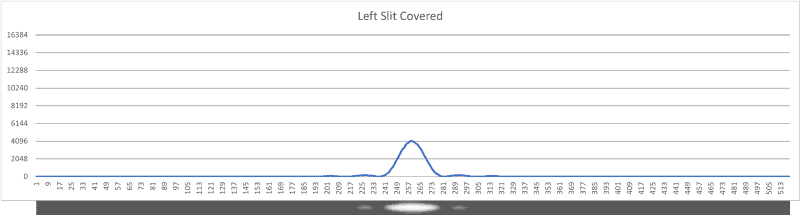
Figure 9: Left slit covered plot.
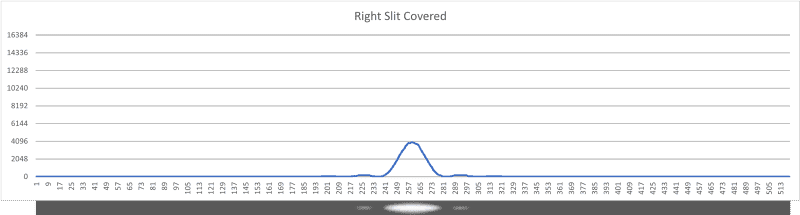
Figure 10: Right slit covered plot.
The shapes of the diffraction/interference patterns also agree with theory.
Notice the central peak of the both slits open plot is interestingly 4 times as high as either single slit plot.
Conservation of energy is all that I require. The rest is your problem.Devin-M said:That’s consistent with conservation of energy, but how do you rule out destruction of energy in some places and creation of energy in others, proportional to the square of the change of intensity in field strength (ie 2 over lapping constructive waves but 2^2 detected photons in those regions?
Don't forget about phase shifts. A reflected wave gets a phase shift of \pi*. Are there any differences in the total phase shifts between the two beams in question (one on the laser side of the interferometer, and the other on the wall side of the interferometer), even if their path lengths are the same?Devin-M said:Yes at the very end he end he asks the viewer if the path difference of the 2 mirrors is 1/2 wavelength, why does the light going to one screen cancel out and the other add constructively. He doesn’t answer this question and leaves it for the viewer to answer. It seems like before he adds the second detection screen, half the light from the mirrors is going to the screen and the other half is going back to the laser source. When he adds the second detection screen now 1/2 is going to the 1st screen, 1/4th is going to the 2nd screen, and 1/4th is going back to the laser. As far as why on one screen there’s a half wavelength path difference and the other there isn’t, I believe it’s due to the thickness of the beam splitter. It seems there must be an extra half wavelength path length (or odd multiple of 1/2 wavelength) for the light from the left mirror that goes back through the beam splitter. I’m not yet fully convinced that when the light cancels out its really going back to the source because once its adding destructively the path length back to the source should be identical all the way back to the source so it should add destructively all the way back to the source.
For example with a different thickness beam splitter it may be possible to have the light on both detection screens add constructively at the same time or both destructively at the same time.
On wikipedia it says “Also, this is referring to near-normal incidence—for p-polarized light reflecting off glass at glancing angle, beyond the Brewster angle, the phase change is 0°.”collinsmark said:Don't forget about phase shifts.
Devin-M said:On wikipedia it says “Also, this is referring to near-normal incidence—for p-polarized light reflecting off glass at glancing angle, beyond the Brewster angle, the phase change is 0°.”
https://en.m.wikipedia.org/wiki/Reflection_phase_change
collinsmark said: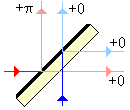
Phase shift through a beam splitter with a dielectric coating.
Source: https://en.wikipedia.org/wiki/Beam_splitter#Phase_shift
provided the reflection is on the side of the medium with the larger index of refraction.collinsmark said:Don't forget about phase shifts. A reflected wave gets a phase shift of \pi*. Are there any differences in the total phase shifts between the two beams in question (one on the laser side of the interferometer, and the other on the wall side of the interferometer), even if their path lengths are the same?
*(For the purposes here, ignore the nuances about reflections caused by the glass itself -- the reflections going from one index of refraction to another. That makes things things overly complicated, and can be ignored for this discussion. A good beam splitter will have coatings to minimize these types of reflections anyway. Instead, treat all reflections as being caused solely by the very thin, half mirrored surface -- the light either gets reflected with a phase shift of \pi, or it gets transmitted with no phase shift at all.)