Does speed vary with a circle's radius?

[mike427]

Hey everyone,

I am not physics major and I haven't had a physics class in sometime, but for my senior project I made a spinning LED display. The original design we had was flat and had an array of leds that blinked on and off fast while the motor spun.

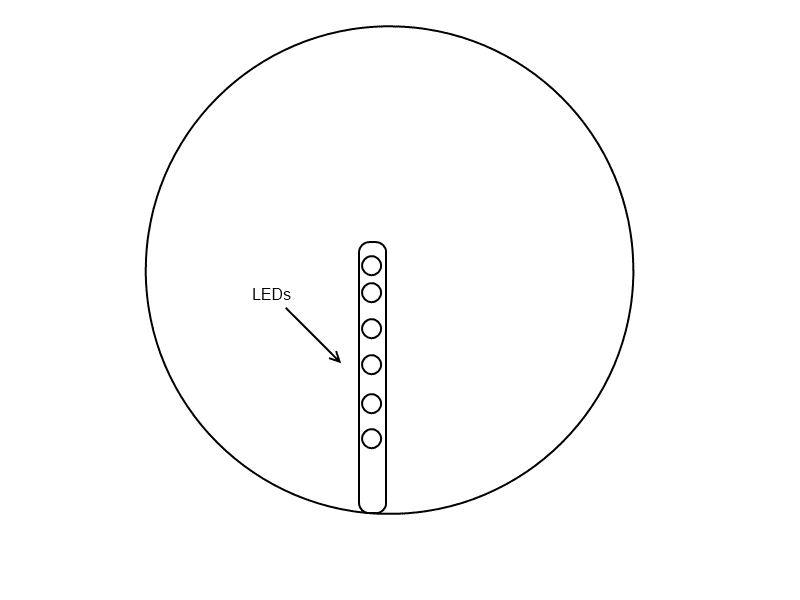
However, when it started to spin and we programmed the letter H, where all of the leds would blink on, then the center would only be on, and the all of them would be lite again we ran into a problem. Here is what it was suppose to look like:

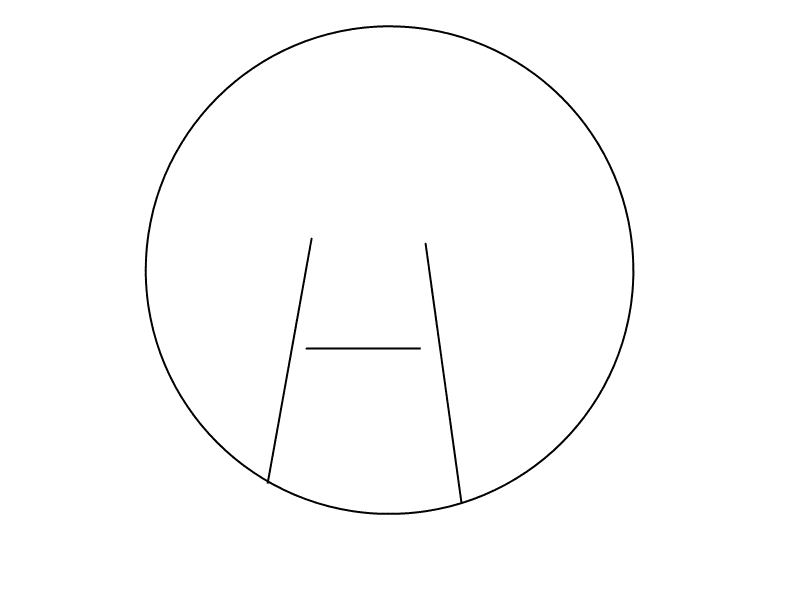
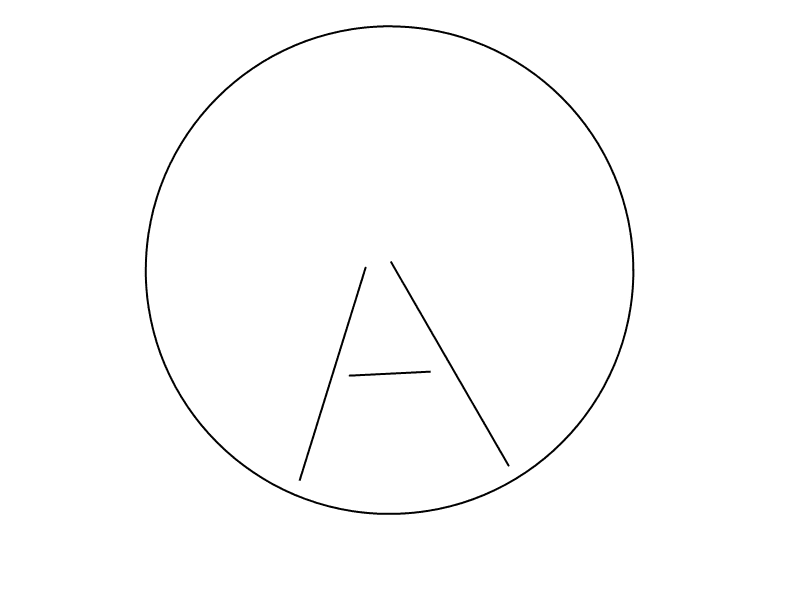
The problem was that it seemed that the center LEDs were somehow spinning faster in the center than the ones on the outside compared to the LEDs on the inside. Basically, instead of an H we got an A:

We ended up standing the LEDs up vertically to create a hologram effect in the end. In addition, having them aligned vertically the same distance from the circle removed that problem.

I recently started discussing my previous dilemma with a friend and I said that the LEDs must have spun faster in the center of the circle. However, he though that the outside would be spinning faster since it covered more distance. Furthermore, we also thought that they should be spinning at the same speed.

So, basically, how does the speed, velocity, or generally any term you want to call it vary to create this effect we saw on the spinning LED display?

 

[berkeman]

Welcome to the PF.

The outer LEDs have a higher linear velocity. All the LEDs have the same angular velocity. The linear velocity V is related to the angular velocity omega by this:

V = R * \omega

Where omega is the angular velocity in radians per second, and R is the radius out to the LED. There are 2*PI radians in a full circle.

As to why your H turned into an A, draw a diagram of concentric circles that show where the LEDs are, and then overlay the H that you want to spell out. Do you see now that you need to turn on different LEDs at different parts of the rotation to trace out the straight lines of the H? (especially the two side legs)

 

[mike427]

Thanks for the response. So basically, its because of the way the circle naturally expands out with two lines out from the center? It was not due to any sort of speed or velocity differentiation?

 

[berkeman]

Thanks for the response. So basically, its because of the way the circle naturally expands out with two lines out from the center? It was not due to any sort of speed or velocity differentiation?

Correct. As long as the rotation frequency is faster than the "flicker fusion frequency" of the human eye, the image will appear steady. The trick is to overlay your letter on the concentric circles to figure out what LEDs need to be on at what times (at what angles of the rotating rod).