Aziza
- 189
- 1
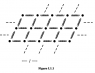
Just started with QFT from Zee and am already confused by first equation lol. See attached picture. Does anyone actually understand this? He calls q_a the vertical displacement of particle 'a', and yet he only allows the springs to be horizontally between the particles. So, there should be no vertical displacement. Unless he envisions the mattress as oriented vertically...but that would be unnecessarily silly.
Also, why is he summing twice over the product of q's in the second term in the lagrangian? If the only springs are horizontally between the particles, and we are actually looking at horizontal instead of vertical displacement, then this second term should be,
∑(kab)(qa-qb)
I don't think this is a typo however, as the third term also contains a product.
I also attached his drawing of a mattress. Clearly in this configuration the only motion is horizontal, not vertical.
Also, why is he summing twice over the product of q's in the second term in the lagrangian? If the only springs are horizontally between the particles, and we are actually looking at horizontal instead of vertical displacement, then this second term should be,
∑(kab)(qa-qb)
I don't think this is a typo however, as the third term also contains a product.
I also attached his drawing of a mattress. Clearly in this configuration the only motion is horizontal, not vertical.
Attachments
Last edited: