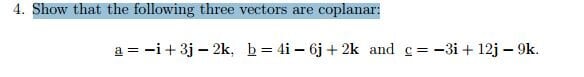Does the triple product being zero guarantee coplanarity of vectors?

[evinda]

Hello! (Wave)

View attachment 5341

Does it suffice to show that the triple product is 0?

If we show that $a \cdot (b \times c)=0$ we will have that $a$ is orthogonal to $b \times c$. $b \times c$ is orthogonal to both $b$ and $c$, so we will have that $a$ will be parallel to $b$ and $c$.
Right? But why does this imply that the vectors are coplanar?

 

[I like Serena]

Hello! (Wave)

Does it suffice to show that the triple product is 0?

If we show that $a \cdot (b \times c)=0$ we will have that $a$ is orthogonal to $b \times c$.

Hey evinda! (Smile)

If we have 3 non-zero vectors, there are 3 possibilities:

1. They are on the same line (all pairs are parallel).
2. They are in the same plane.
3. They span the whole 3-dimensional space (independent of each other).

Let's start with $b$ and $c$.
If they are on the same line, their cross product is zero.
Then it doesn't matter what $a$ is, in all cases we will have $a \cdot (b \times c)=0$.
So we cannot immediately say that $a$ is orthogonal to $b\times c$. (Nerd)

Are $b$ and $c$ on the same line?

$b \times c$ is orthogonal to both $b$ and $c$, so we will have that $a$ will be parallel to $b$ and $c$

Let's assume that $b$ and $c$ are independent, then they span a plane, and $b \times c \ne 0$.

You seem to be saying that $a$ is parallel to $b$, but that is not true. (Worried)
We would have that $a$ is in the same plane as $b$ and $c$.
Or put otherwise, that $a$ is a linear combination of $b$ and $c$.
That is, coplanar. (Nerd)

 

[evinda]

If we have 3 non-zero vectors, there are 3 possibilities:

1. They are on the same line (all pairs are parallel).
2. They are in the same plane.
3. They span the whole 3-dimensional space (independent of each other).

Why are there these possibilities? And why are these the only ones?

Let's start with $b$ and $c$.
If they are on the same line, their cross product is zero.
Then it doesn't matter what $a$ is, in all cases we will have $a \cdot (b \times c)=0$.
So we cannot immediately say that $a$ is orthogonal to $b\times c$. (Nerd)

Are $b$ and $c$ on the same line?

No, since the one isn't a multiple of the other. So we reject the first case, right?

Let's assume that $b$ and $c$ are independent, then they span a plane, and $b \times c \ne 0$.

Does it hold that two vectors $b$ and $c$ are linearly independent iff $b \times c \ne 0$ ?

Also would it hold that they span a plane because a plane is a subset of $\mathbb{R}^2$ and any two linearly independent vectors span a subspace of $\mathbb{R}^2$ ?

Also isn't the equation of a plane of the form $A(x-x_0)+B(y-y_0)+C(z-z_0)=0$ ? WHy can we say that it is a subset of $\mathbb{R}^2$ ?

You seem to be saying that $a$ is parallel to $b$, but that is not true. (Worried)
We would have that $a$ is in the same plane as $b$ and $c$.
Or put otherwise, that $a$ is a linear combination of $b$ and $c$.
That is, coplanar. (Nerd)

What would we deduce that $a$ is in the same plane as $b$ and $c$? (Sweating)

 

[I like Serena]

Why are there these possibilities? And why are these the only ones?

Not sure what you're looking for here... (Wondering)

Let's try this: each sub space of $\mathbb R^3$ must be isomorphic to one of $\mathbb R^0$ (a point), $\mathbb R^1$ (a line), $\mathbb R^2$ (a plane), or $\mathbb R^3$ (the whole space).

No, since the one isn't a multiple of the other. So we reject the first case, right?

Yep. (Nod)

Does it hold that two vectors $b$ and $c$ are linearly independent iff $b \times c \ne 0$ ?

Also would it hold that they span a plane because a plane is a subset of $\mathbb{R}^2$ and any two linearly independent vectors span a subspace of $\mathbb{R}^2$ ?

Also isn't the equation of a plane of the form $A(x-x_0)+B(y-y_0)+C(z-z_0)=0$ ? WHy can we say that it is a subset of $\mathbb{R}^2$ ?

It holds for non-zero vectors.

A plane in $\mathbb R^3$ is not a subset of $\mathbb{R}^2$.
Instead it's isomorphic to $\mathbb{R}^2$, implying there is a bijection between them.

What would we deduce that $a$ is in the same plane as $b$ and $c$? (Sweating)

If $b$ and $c$ are independent, they span a plane through the origin.
If the vector $(A,B,C)$ is normal to that plane, the equation of the plane is:
$$(A,B,C) \cdot (x,y,z) = Ax+By+Cz=0$$
Note that these are exactly all vectors that are perpendicular to $(A,B,C)$.
So if $a$ is perpendicular to a normal of the plane, it must therefore be in the plane. (Nerd)