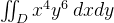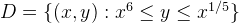SUMMARY
This discussion focuses on solving the x limits for the area bounded by the curves \(y=x^6\) and \(y=x^{1/5}\). The intersection points of these curves are determined to be \(x_1=1\) and \(x_2=0\). The double integral is set up as \(\int_0^1\int_{x^6}^{x^{\frac{1}{5}}} x^4y^6 \, dy \, dx\), which is solved using Fubini's theorem. The final result of the integral evaluates to \(\frac{29}{1504}\).
PREREQUISITES
- Understanding of double integrals and their applications
- Familiarity with Fubini's theorem
- Knowledge of polynomial functions and their intersections
- Basic integration techniques in calculus
NEXT STEPS
- Study the application of Fubini's theorem in multi-variable calculus
- Learn how to find intersections of polynomial curves
- Explore advanced integration techniques for solving double integrals
- Practice solving double integrals with varying limits
USEFUL FOR
Students and educators in calculus, mathematicians focusing on integration techniques, and anyone looking to deepen their understanding of double integrals and polynomial intersections.
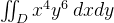 ,
,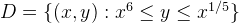 Regards,
Regards,