Double pendulum - solving with energy and Simulink

[aaddcc]

Hi everyone,

I am trying to familiarize myself with Simulink by graphically drawing out differential equations, but ran into a snag with a double pendulum on a cart. Anyways, I neglect friction or other damping effects and say that

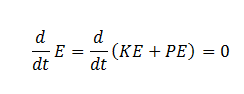
From there I simply just sum the energies, which ends up as:

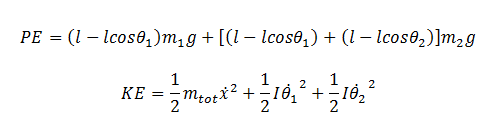
And then differentiating with respect to time ends up with:

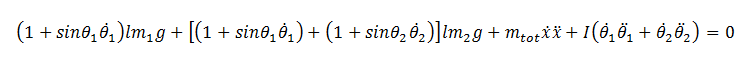
This seemed fine to me, and I started creating my Simulink model. The way that works is I have a loop with each variable connecting to each other in a certain way (i.e. xddot = stuff, thetaddot = other stuff). The issue is, when solving for any of the second order derivatives it is necessary to divide by the first order derivative. For example, to solve for the acceleration of x it is necessary to divide by the velocity of x. What if the velocity happens to be zero? In that case my Simulink model fails.

I did it with energy because it seemed a lot easier. Is there any other way to isolate the variables without dividing by terms like velocity which could be zero?

 

[timthereaper]

It might be easier to form the Lagrangian and just use the Euler-Lagrange equations and put those differential equations in Simulink. I've done some Simulink models for control systems of inverted pendulums and haven't had any problems separating out the double derivatives in matrix form.

This link contains all the derivations, so hopefully you can just plug it in and get something:
http://scienceworld.wolfram.com/physics/DoublePendulum.html

Hope that helps!