Double slit experiment light distance

[Violagirl]

Homework Statement

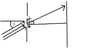
Suppose that light is incident on a double slit apparatus, with a slit separation d at an angle of ∅ (phi) to the normal (see attached diagram). A) Derive an equation; in terms of the variables d, ∅, θ, integers m, and the wavelength λ of the incoming light; that yields the location of the maxima (constructive interference). B) If ∅ = 20°, what is the angle θ of the m = 0 central maximum? C) If the wavelength of the incoming light is 500 x 10^-9 m, the slit separation is 0.25 mm, and the distance to the screen is D = 10 m, how far form the central (m = 0) maximum is the nearest (m - 1) maximum?

Homework Equations

Constructive interference:
δ_tot = mλ

d sin θ = mλ

d sin ∅ = mλ

The Attempt at a Solution

Diagram of situation is attached. I'm confused on this one. I understand constructive interference but am a little confused on the derivation. I know that the wavelengths corresponding to ∅ and θ both travel an extra distance of d sin ∅ and d sin θ which then must correspond to mλ but how are they connected all together? Any input is appreciated.

 

[BeBattey]

First off you are going to have a phase difference between the two rays as they strike the slits. Past this you can tack on the distance each individual ray goes, to factor in the second phase difference. These two phase differences must both be accounted for to get a function for constructive/deconstructive interference.

 

[haruspex]

Can't you treat it as though the angle just makes the slits effectively a little closer, the screen a bit further away, and the lines on the screen a bit further apart?

 

[BeBattey]

No, because interference has to do with total distance traveled. You just have to pick a point at which you KNOW the two rays are in phase, then figure out the total distance traveled of each ray as a function of the angles, find their difference, and if they are a multiple of the wavelength, you have constructive, etc.

It's all about total distance traveled.

 

[haruspex]

It's all about total distance traveled.

Well, it's to do with the difference in path lengths. I don't see that it invalidates my method. The only thing my method gets wrong is that the two slits are now at slightly different distances along the path from source to target, but that will make very little difference.