- #1
ab200
- 13
- 3
- Homework Statement
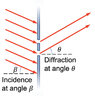
- Suppose that a laser beam hits a double-slit apparatus at an angle of β = 40 degrees with respect to the normal. The screen is a distance L away, with slit width a and slit separation d.
Derive a symbolic expression for locating the double-slit interference maxima. At what angle θo is the center of the interference pattern located on the screen? Is the interference pattern symmetric about that angle?
- Relevant Equations
- dsinθ = mλ (maxima)
tanθ = ym / L
Given that [y][/m] is equal to the position of the interference maxima and is the variable I’m solving for. I got as far as setting up two expressions, one for sinθ and the other for tanθ.
sinθ = (mλ)/d
tanθ = ym/L
My first instinct was to set θ = 40 degrees. By relating sinθ and tanθ to each other through cosθ, I get:
ym = (Lmλ) / (dcos40)
However, I don’t think this makes sense if I have to solve for θo in the second part of the question, so θ must not be fixed. I’m confused about how I am supposed to use the given value of β, but I assume it must be relevant.
If I were able to use small-angle approximation, sinθ ≈ tanθ, but does this still apply here?
sinθ = (mλ)/d
tanθ = ym/L
My first instinct was to set θ = 40 degrees. By relating sinθ and tanθ to each other through cosθ, I get:
ym = (Lmλ) / (dcos40)
However, I don’t think this makes sense if I have to solve for θo in the second part of the question, so θ must not be fixed. I’m confused about how I am supposed to use the given value of β, but I assume it must be relevant.
If I were able to use small-angle approximation, sinθ ≈ tanθ, but does this still apply here?