- #1
kcurse21
- 9
- 0
- Homework Statement
- If Gn is the nth stage of the construction then Gn+1 = f1(Gn) ∪ f2(Gn) ∪ f3(Gn).
Beginning with the unit interval sketch the next three stages of the construction and calculate the fractal/box counting dimension of the object as n → ∞.
- Relevant Equations
- Let X = [0, 1]. Consider the Iterated Function System
f1(X) = 1/3X
f2(X) = 1/3X+1/3(1,1)
f3(X) = 1/3X+2/3(1,0)
Attempt
The interval sketch is obviously a line from 0, 1.
F1 would cut the interval line by a third similar to the Cantor set.
F2 would cut the interval line by a third and then there is a transformation that moves to the point (1/3, 1/3).
F3 would cut the interval line by a third and then there is a transformation that moves to the point (2/3, 0).
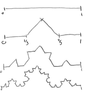
Based on the cantor set, you would assume that the third would be placed underneath the interval sketch but my problem arises with f2. F3 I'm assuming you cut the interval sketch by a third at the point (2/3, 0) which would give you the other side of the cantor set per se. But I have no idea what to do with F2 and how to draw this as a whole. I will provide a sketch of the Koch curve so it is understood what I mean.
The interval sketch is obviously a line from 0, 1.
F1 would cut the interval line by a third similar to the Cantor set.
F2 would cut the interval line by a third and then there is a transformation that moves to the point (1/3, 1/3).
F3 would cut the interval line by a third and then there is a transformation that moves to the point (2/3, 0).
Based on the cantor set, you would assume that the third would be placed underneath the interval sketch but my problem arises with f2. F3 I'm assuming you cut the interval sketch by a third at the point (2/3, 0) which would give you the other side of the cantor set per se. But I have no idea what to do with F2 and how to draw this as a whole. I will provide a sketch of the Koch curve so it is understood what I mean.
Attachments
Last edited: