SUMMARY
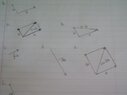
The discussion focuses on vector drawing techniques, specifically using the parallelogram law and vector subtraction. Participants confirm the correctness of vector orientations, particularly for parts (a), (b), and (f). The consensus is that vector b can be represented as -b when flipped, and the resultant vector for part (f) is constructed by connecting 2b and -a head to tail. Visual aids, such as the parallelogram law diagram, are referenced to enhance understanding.
PREREQUISITES
- Understanding of vector addition and subtraction
- Familiarity with the parallelogram law in vector mathematics
- Basic knowledge of vector notation and representation
- Ability to visualize geometric concepts in two dimensions
NEXT STEPS
- Study the properties of vector addition and subtraction in detail
- Learn how to apply the parallelogram law to various vector problems
- Explore visual representation techniques for vectors in geometry
- Practice drawing vectors using different orientations and connections
USEFUL FOR
Students and educators in mathematics, particularly those focusing on geometry and vector analysis, as well as anyone seeking to improve their skills in drawing and visualizing vectors accurately.