- #1
spacetimedude
- 88
- 1
I am trying to determine the contour required in solving part b. The branch points (poles) are at s=0 and s= -a and in between these two values, there is a branch cut.
I know that the branch cut cannot be included in the contour so does this mean the poles also cannot be in the contour? Would it be the one shown in the second image?
Thank you.
EDIT: Got branch points and poles mixed up. Reattempting now.
EDIT2: Hmm, are the branch points the same as poles in this case? Clarification would be appreciated.

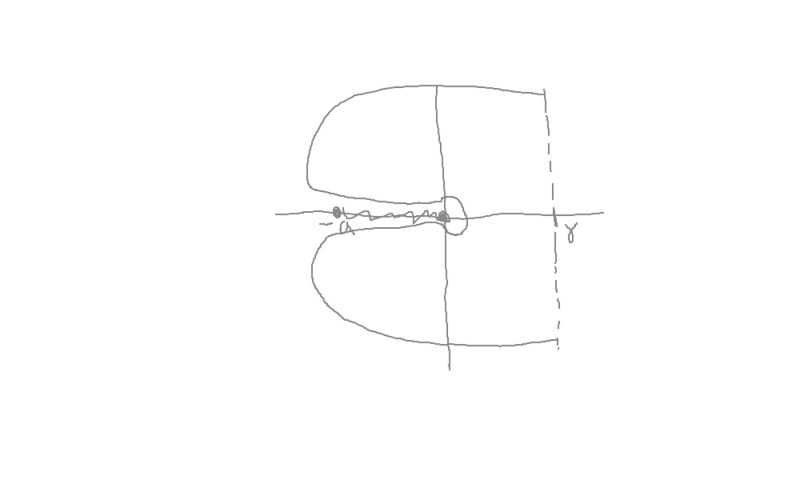
I know that the branch cut cannot be included in the contour so does this mean the poles also cannot be in the contour? Would it be the one shown in the second image?
Thank you.
EDIT: Got branch points and poles mixed up. Reattempting now.
EDIT2: Hmm, are the branch points the same as poles in this case? Clarification would be appreciated.
Attachments
Last edited:
