Integrating a function of which poles appear on the branch cut

[tworitdash]

I have a complicated function to integrate from $-\infty$ to $\infty$.

$$I = \int_{-\infty}^{\infty}\frac{(2k^2 - \Omega^2)(I_0^2(\Omega) + I_2(\Omega)^2) - \Omega^2 I_0(\Omega) I_2(\Omega)}{\sqrt{k^2 - \Omega^2}} \Omega d\Omega$$​

Where I0I0 and I2I2 are functions containing Hankel functions as below.

$$I_0(\Omega) = \frac{R}{\beta^2 - \Omega^2}\Big(aJ_1(\beta R)H_0^{(2)}(\Omega R) - \Omega J_0(\beta R) H_1^{(2)}(\Omega R)\Big)$$

$$I_2(\Omega) = \frac{R}{\beta^2 - \Omega^2}\Big(-aJ_1(aR)H_2^{(2)}(\Omega R) + \Omega J_2(aR) H_1^{(2)}(\Omega R)\Big)$$​

$H_n^{(2)}$ are Hankle functions of the second kind of order n. $J_n$ are the Bessel function of the first kind and order n. Along with this I also happen to have the expressions when $\beta = \Omega$ and they are,

$$I_0(\Omega) = \frac{1}{2} R^2 \Big( (H_0^{(2)}(\Omega R))^2 + H_1^{(2)}(\Omega R)H_2^{(2)}(\Omega R))\Big)$$

$$I_2(\Omega) = \frac{1}{2} R^2 \Big( (H_2^{(2)}(\Omega R))^2 - H_1^{(2)}(\Omega R)H_3^{(2)}(\Omega R))\Big)$$

The above 2 expressions are valid on only points where $|\Omega| = \beta$ These expressions actually help avoid the poles at those points in the actual expressions of $I_0$ and $I_2$. However, in my question I don't address the pole free expressions.

So, now the square root term is evaluated as $\sqrt{k^2 - \Omega^2} = -j \sqrt{-(k^2 - \Omega^2)}$. And Hankel functions have a logarithmic discontinuity at the origin. I extended it to the negative infinity for a branch cut. Therefore, the branch cuts of the square root and Hankel functions are shown in the figure here.

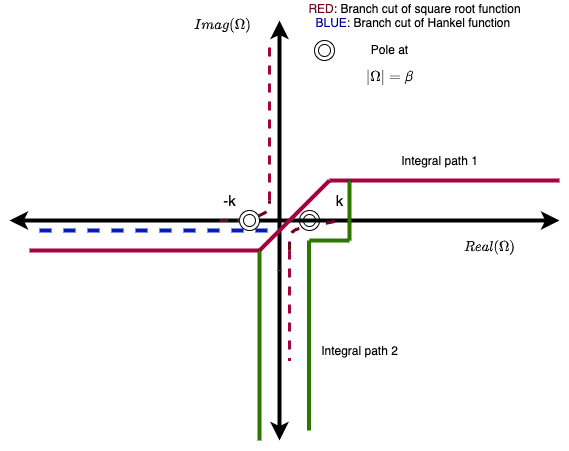
I have tried 2 integration paths. The first path starts from negative infinity (and a small delta below the real axis) on the real axis, goes just below the origin to avoid the branch cut of Hankel function, and moves to positive infinity on the real axis (and a small delta above the real axis). The delta is used to avoid the poles at $\pm \beta$ and at $\pm k$. The second integration path starts from negative imaginary infinity on the third quadrant and follows the same path about the origin but comes to again negative infinity on the imaginary axis in the fourth quadrant after covering the branch-cut of square root just after k on the real axis.In the problem $|\beta| < |k|$ always. Therefore, poles at $\pm \beta$ appear on the branch cut of the square root function. I am not using the pole free expressions for the integrated so the delta makes a huge impact on the integral. The poles lie on the branch cut, so I don't know how to avoid them or how to apply the Cauchy's theorem because one can't move around the pole jumping on the branch cut.

The integral is real when I take the integral only till k and it is purely imaginary when I take the integral from k to $\infty$. This happens because of the square root function. If I change the delta, the real part of the integral changes considerably which makes me think that the poles at $\pm \beta$ and $\pm k$ are responsible. Can I use the pole free expressions? I am afraid I can't because it is only valid at the pole points and not its locality. Please share your thoughts.

 

[tworitdash]

I figured out how to execute this without any warnings. I used pole free expressions at the locality of the pole. I took an offset of e-7 so that it doesn't come very close to the pole location. Furthermore, I didn't use the second integration path I have mentioned in the picture above and used the first integral path, but from 0 to $\infty$. For this reason, I changed all Hankle functions of the second kind to Bessel functions of the first kind. (because that was my original problem and keeping in mind that I can make a faster convergence, I used Hankel function from $-\infty$ to $\infty$)