etotheipi
The parabolic mirror pictured below is such that all incident rays, neglecting diffraction, are reflected towards a focus.
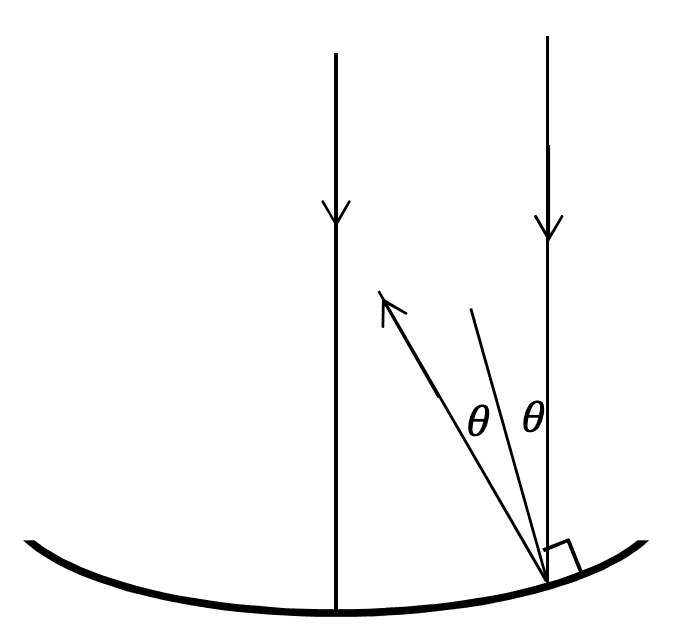
A question states that the light cannot be focused to a point precisely, since there exists a circular diffraction pattern in the focal plane. The following diagram is given:

I'm trying to understand how to calculate the drop in intensity at the image, supposing the intensity of light from the source before it enters the telescope is known. I understand that we can approximate to a reasonable degree of accuracy that only the light in the central maximum within ##\theta = \frac{1.22\lambda}{2}## need be considered; then a ratio of areas can be used for the intensity.
But I can't actually see what ##D## is referring to in the second figure; I assume ##f## is the focal length. Where is the diffraction actually occurring in the parabolic mirror? Thanks!
A question states that the light cannot be focused to a point precisely, since there exists a circular diffraction pattern in the focal plane. The following diagram is given:
I'm trying to understand how to calculate the drop in intensity at the image, supposing the intensity of light from the source before it enters the telescope is known. I understand that we can approximate to a reasonable degree of accuracy that only the light in the central maximum within ##\theta = \frac{1.22\lambda}{2}## need be considered; then a ratio of areas can be used for the intensity.
But I can't actually see what ##D## is referring to in the second figure; I assume ##f## is the focal length. Where is the diffraction actually occurring in the parabolic mirror? Thanks!
Last edited by a moderator: